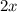 )
)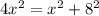
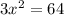
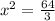
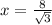
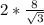 =
=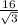
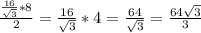 см²
см²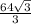 см²
см²
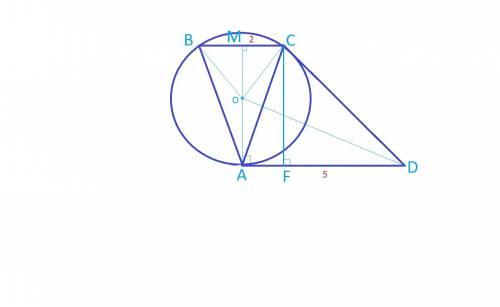
 трапеция
трапеция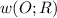 - описана около Δ
- описана около Δ 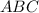
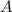 и
и 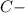 точки касания
точки касания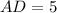
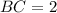
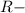 ?
?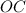 ⊥
⊥ 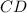
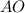 ⊥
⊥ 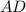
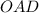 и Δ
и Δ 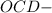 прямоугольные
прямоугольные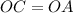 ( как радиусы)
( как радиусы)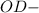 общая
общая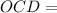 Δ
Δ 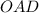 (по гипотенузе и острому углу)
(по гипотенузе и острому углу)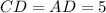
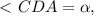 тогда
тогда 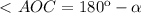
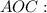
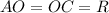

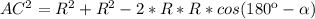
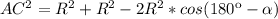
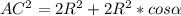


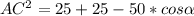
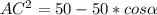
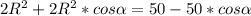
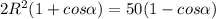
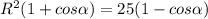
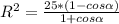
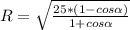 (1)
(1)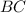 ║
║ 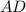
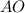 ⊥
⊥ 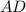
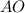 ∩
∩ 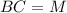 ⇒
⇒ 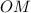 ⊥
⊥ 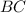
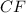 ⊥
⊥ 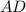
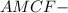 прямоугольник
прямоугольник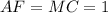
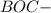 равнобедренный, значит
равнобедренный, значит 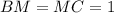
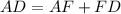
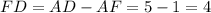
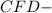 прямоугольный
прямоугольный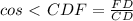
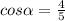
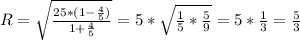
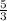
AB II РМ.
2. Проведем отрезок EF. Рассмотрим треугольники EKF и РКМ. Они подобны по второму признаку подобия треуг-ов: две стороны одного треуг-ка пропорциональны двум сторонам другого треуг-ка и углы, заключенные между этими сторонами, равны. В нашем случае:
- КЕ : КР = 1 : 3 (откуда взялось 3: КР=КЕ+ЕР=1 часть + 2 части=3 части);
- KF : KM = 1 : 3 (точно также КМ=KF+FM=1 часть+2 части=3 части);
- угол К, заключенный между пропорциональными сторонами, - общий.
У подобных треугольников соответственные углы равны: <EFK=<PMK
3. Рассмотрим эти углы. Это соответственные углы при пересечении двух прямых EF и PM секущей КМ. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Т.е.
EF II PM.
4. Выше мы вывели, что РМ II AB, значит EF II АВ.
Итак, мы доказали, что две стороны четырехугольника ABEF параллельны.
5. Построим отрезок NK. Рассмотрим треугольники NMK и NPK. Здесь ни AF, ни BE не будут являться средними линиями этих треугольников, поскольку точка F не является серединой стороны КМ, так же, как и точка Е - не середина стороны РК. Значит, они непараллельны основанию KN, которое является общим для обоих треугольников. Они непараллельны и между собой.
В итоге мы получаем, что четырехугольник ABEF имеет две параллельные стороны и две непараллельные стороны. Значит это - трапеция.