1.Пусть дана трапеция АВСД, чтобы найти периметр, НЕ ХВАТАЕТ только стороны АВ, которая равна высоте СТ, проведенной к стороне АД из вершины С. Точка Т лежит на АД, т.к. СТ⊥АД, то по теореме Пифагора из ΔСТД найдем СТ=√(20²-16²)=√(36*4)=12, значит периметр равен
АД+ВС+СД+АВ=25+9+20+12=66/см/
2.Большая диагональ лежит против тупого угла С, тогда меньшая диагональ АС, которую найдем из ΔАВС ;
АС=√(АВ²+ВС²)=√(12²+9²)=√(144+81)=15/см/
3.В треугольнике АСД стороны АС=15; СД=20; АД=25, и связаны между собой таким отношением -квадрат большей стороны равен сумме квадратов двух других, действительно, 25²=20²+15²,625=400+225, но тогда по теореме, обратной теореме Пифагора треугольник АСД - прямоугольный с прямым углом С, а раз так, То АС- расстояние от точки А до прямой СД, это расстояние ρ(A;CD) равно АС=15см
30
Объяснение:
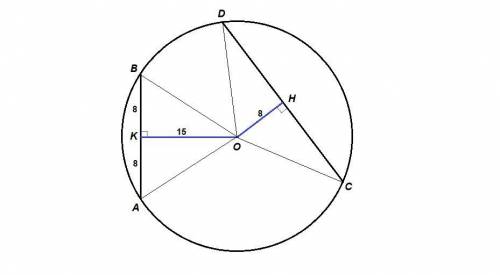
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30
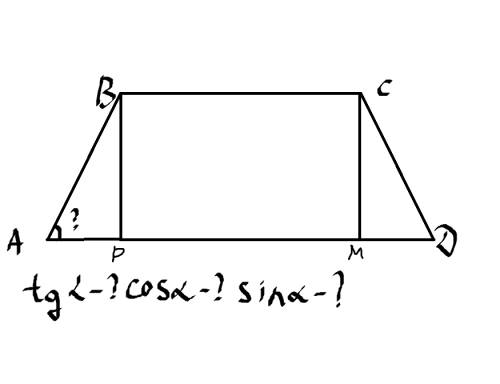
Дано:
AD-BC=8см
AB+CD=10см
sin a-?
cos a-?
tg a-?
Решение
1) Проведем перпиндекуляры из углов B и C к основанию AD
2) Т.к. по условию AD-BC=8 см, то AP+MD+PM-BC=8 см
3) Рассмотрим треугольники ABP и CMD. Они равны по 1 признаку:
1) BP=CM (как перпендикуляры проведенные из равных по величине углов)
2) угол A=D (как углы при основании равнобедренной трапеции)
3) AB=CD (как стороны равнобедренной трапеции)
4) Т.к. треугольники ABP и CMD равны, то AP=MD. Т.к. BC=PM, AP=MD то
AP+MD+PM-BC=8 см
2AP=8 см
AP=4 см
5) AB+CD=10 см - по условию
Т.к. стороны равнобедренной трапеции равны, то
2AB=10 см
AB=5 см, следовательно и CD=5 см
6) Т.к. AB=5 см, AP=4 см, то по теореме Пифагора:
BP=корень (AB^2-AP^2)=корень (25-16)=3 см
7) sin a= BP\AB=3\5=0,6 (синус-отношение противолеж. катета к гипотенузе)
cos a= AP\AB=4\5=0,8 (косинус-отношение прилежащего катета к гипотеннузе)
tg a= BP\AP=0,75 (тангенс-отношение противолеж. катета к прилежащему)
ответ: sin a=0,6 ;cos a=0,8 ;tg a=0,75.
Объяснение: 1)проведем высоту СН=АВ НД=25-9=16
из прямоуг.ΔСНД СН^2=20^2-16^2=144 CH=12=AB
периметр P=12+9+20+25=66
2)ΔABC-прямоуг. , АС^2=AB^2+BC^2=12^2+9^2=225 AC=15
3) ΔACD-прямоуг. так как 25^2=20^2+15^2→расстояние от точки A до прямой CD равно AC=15