Полученный четырехугольник - ромб.
Объяснение:
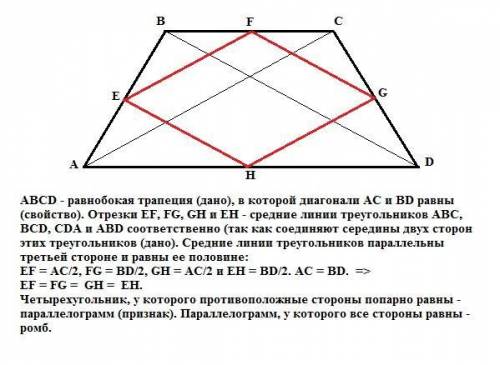
ABCD - равнобокая трапеция (дано), в которой диагонали АС и BD равны (свойство). Отрезки EF, FG, GH и EH - средние линии треугольников АВС, BCD, CDA и ABD соответственно (так как соединяют середины двух сторон этих треугольников (дано). Средние линии треугольников параллельны третьей стороне и равны ее половине:
EF = АС/2, FG = BD/2, GH = AC/2 и EH = BD/2. AC = BD. =>
EF = FG = GH = EH.
Четырехугольник, у которого противоположные стороны попарно равны - параллелограмм (признак). Параллелограмм, у которого все стороны равны - ромб.
Враховуючи, що у подібних трикутників сторони відносяться однаково, маємо, що 7 - 3 = 4 частини припадає на різницю 32. Звідси на одну частину припадає 32:4 = 8 одиниць довжини (можливо см). Отже, сторони подібного трикутника, відповідно, дорівнюють: 7·8 = 56; 6·8 = 48; 3·8 = 24 одиниць довжини.
Відповідь: 56; 48; 24.