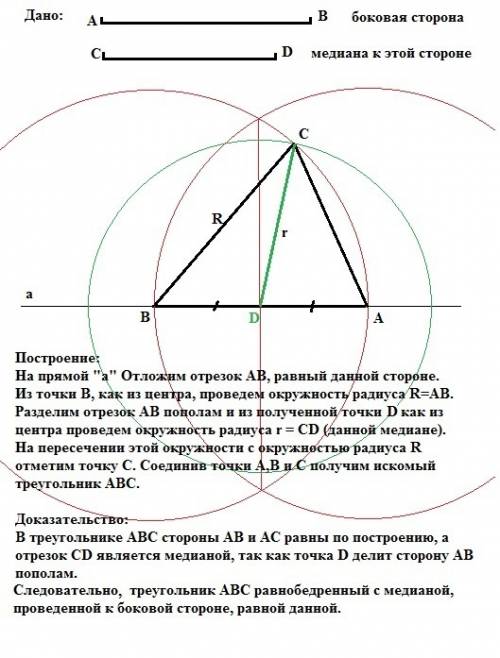
Построение:
На прямой "а" Отложим отрезок АВ, равный данной стороне. Из точки В, как из центра, проведем окружность радиуса R=AB. Разделим отрезок АВ пополм, отметим середину отрезка точкой D и из полученной точки D как из центра проведем окружность радиуса r = CD (равного данной медиане). На пересечении этой окружности с окружностью радиуса R отметим точку С. Соединив точки А,В и С получим искомый треугольник АВС.
Доказательство:
В треугольнике АВС стороны АВ и АС равны по построению, а отрезок CD является медианой, так как точка D делит сторону АВ пополам. Следовательно треугольник АВС равнобедренный с медианой, проведенной к боковой стороне, равной данной.
Если 2 стороны и угол между ними одного треугольника соответственно равны 2 сторонам и углу между ними другого треугольника ,то такие треугольники равны
2 признак.
Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней угла другого треугольника,то такие треугольники равны.