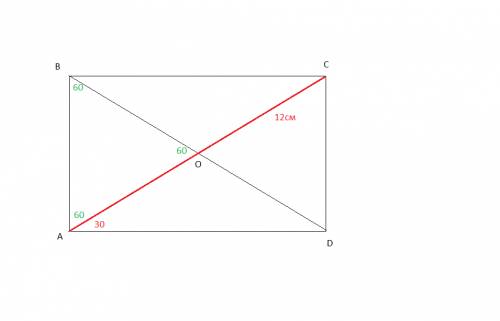
сделаем построение по условию
АС=12см тогда АО=12/2=6см
<CAD=30 тогда смежный <OAB =60
треугольник АВО -равносторонний -все углы равны 60 -все стороны равны 6 см
тогда ПЕРИМЕТР =3*6=18 см
ответ 18см
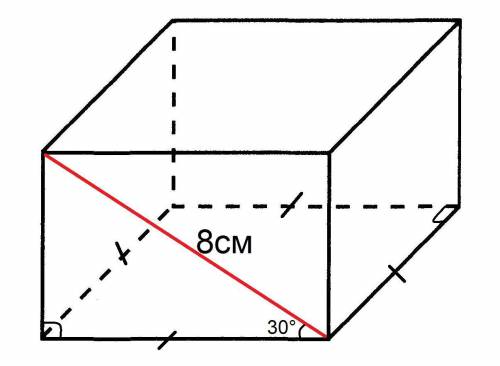
Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.
угол ВАО=90-30=60 гр
в прямоугольнике диагонали равны, АС=BD=12см
и пересекаются в середине, АО=ВО=6см
тр-к АОВ равносторонний, т к АО=ВО и угол ВАО=60 гр
следовательно периметр P=6*3=18 cм