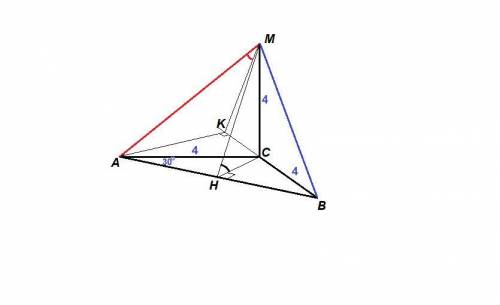
a) tg∠MHC = 2
б) ∠(AM; (MBC)) = arccos(√10/4)
Объяснение:
a) Пусть Н - середина АВ, тогда СН - медиана и высота равнобедренного треугольника АВС,
СН ⊥ АВ.
СН - проекция МН на плоскость (АВС), значит
МН ⊥ АВ по теореме о трех перпендикулярах.
Тогда ∠МНС - линейный угол двугранного угла МАВС.
Из прямоугольного треугольника АСН:
СН = АС/2 = 2 см, как катет, лежащий против угла в 30°.
ΔМНС: ∠МСН = 90°,
tg∠MHC = MC / CH = 4 / 2 = 2
б) ∠ВАС = ∠ВСА = 30° как углы при основании равнобедренного треугольника АВС, ⇒
∠АСВ = 180° - 30° · 2 = 120°
Проведем АК⊥ВС, тогда ∠ АСК = 180° - 120° = 60° (по свойству смежных углов).
ΔАСК: ∠АКС = 90°
∠САК = 90° - 60° = 30°.
КС = 1/2 АС = 2 см как катет, лежащий против угла в 30°.
ΔСКМ: ∠МСК = 90°, по теореме Пифагора
МК = √(МС² + СК²) = √(16 + 4) = √20 = 2√5 см
СМ⊥(АВС) по условию, значит
СМ⊥АК,
АК⊥ВС по построению, ⇒ АК ⊥ (МВС), тогда
МК - проекция прямой АМ на плоскость (МВС) и значит
∠АМК = ∠(АМ; (МВС)) - искомый.
ΔАМС прямоугольный равнобедренный, значит его гипотенуза
АМ = СМ√2 = 4√2 см
ΔАМК: ∠АКМ = 90°
cos∠AMK = MK / AM = 2√5 / (4√2) = √10/4
∠AMK = arccos(√10/4)
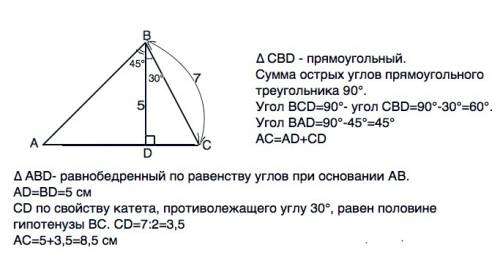
Дано: угол CDB=90°, угол ABD= 45°, угол CBD= °,. BC= 7 см, BD= 5 см. Найти: угол A, угол C, AC.
————
Сделаем по данному условию рисунок и рассмотрим прямоугольные треугольники АВD и СВD, на которые ВD разбила исходный.
Сумма острых углов прямоугольного треугольника 90°.
∠ВАD=90°- 45°=45°
⊿ АВD- равнобедренный по равенству углов при основании АВ ⇒ АD=BD=5 см
∠CDB=90°и угол СВD=30°(дано),⇒ В ⊿ ВСD ∠С=90°-30°=60°.
Длина отрезка равна сумме длин составляющих его частей⇒ АС=AD+CD
Катет прямоугольного треугольника, противолежащий углу 30°, равен половине гипотенузы. ⇒ CD=1/2•BC=7:2=3,5 см, из чего следует: АС=АD+DC=5+3,5=8,5 см.
НО!
По т.Пифагора квадрат гипотенузы равен сумме квадратов катетов. ⇒ СD=√(BC²-ВD²)=√24=2√6, и не равно 3,5
Следовательно, треугольник ВСD с гипотенузой 7 и катетом 5 не может иметь острый угол 30°, если он прямоугольный.
Величина угла СВD -по ошибке или намеренно ( бывает и так), - дана неверно.
Найдем искомый угол C по его синусу.
sinC=ВD/BC=5/7=0.7142857142857143 По таблице Брадиса или по калькулятору находим его величину. ∠С=45,58° .
Тогда СD=BC•cos45,58°=7•0,6999≈4,9 см ⇒
АС=5+4,9≈9,9 см.
.
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:
Вычислим стороны
т.е. АВ = АС, следовательно треугольник равнобедренный. Что и требовалось доказать
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Точка D(-6;4)
Длину высоты можно вычислить и по другой формуле, как расстояние между точкой A(-6;1) и точкой D(-6;4).