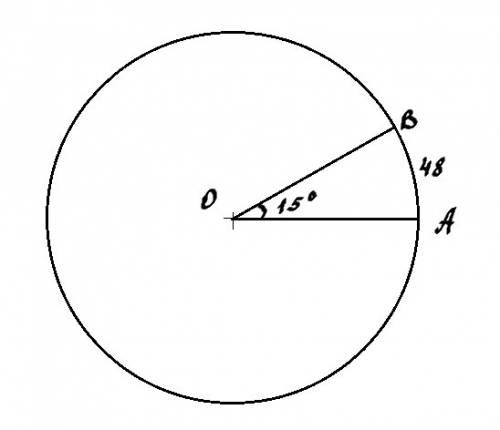
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.
АВ=АМ.
<CKD=<ADK как накрест лежащие углы при пересечении двух параллельных прямых ВС и AD секущей KD. Но <ADK=<CDK, т.к. DK - биссектриса, значит <CKD=<CDK. Треугольник CKD получается равнобедренным с равными углами при его основании DK.
CD=CK
Т.к. ABCD - параллелограмм, то АВ=CD. Но мы выше вывели, что АВ=АМ, а CD=CК, значит
АМ=СК
Треугольники АМВ и CKD получаются равны по двум сторонам и углу между ними: АВ=CD, АМ=СК, углы А и С равны как противоположные углы параллелограмма.
2. ВК=ВС-СК, DM=AD-АМ. Поскольку ВС=AD, а СК=АМ (как равные соответственные стороны равных треугольников АМВ и CKD), то ВК=DM. Эти отрезки лежат на параллельных сторонах ВС и AD, значит, они также параллельны. Значит, BKDM - параллелограмм (две стороны равны и параллельны), следовательно, ВМ II DK.