Для решения применим теорему Фалеса: Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Чтобы без линейки с делениями разделить отрезок, длина которого не известна, нужно от одного из концов этого отрезка провести под углом к нему вс луч и на этом луче на равном расстоянии отметить нужное количество точек.
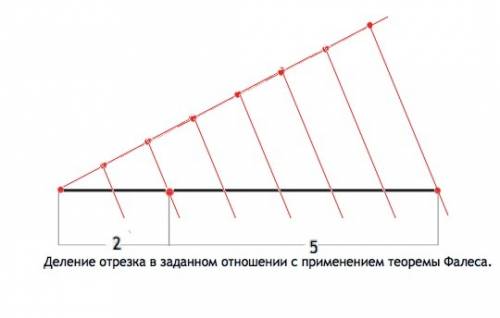
а) На вс луче отложим через равные промежутки 2+5 =7 точек. Затем через последнюю точку и конец заданного отрезка проведём прямую и через все точки ещё 6 прямых, параллельных ей. При этом заданный отрезок будет разделен на 7 равных частей. Отсчитаем 2 из получившихся отрезков. Остальная часть равна 5 отмеренным отрезкам, а исходный разделен в отношении 2:5
Можно на заданном отрезке откладывать не 7 отрезков, а провести всего 2 прямые - через седьмую и параллельно ей через вторую точку. Заданный отрезок будет разделён в нужном отношении.
б) и в) делим точно так же.
Нехай вершина піраміди S , а вершини трикутника в основі А,В,С
Основа правильної трикутної піраміди - правильний трикутник.
Площа правильного трикутника дорівнює a^2*корінь(3)/4, де а - сторона трикутника
Площа трикутника АВС дорівнює 18^2*корінь(3)/4=81*корінь(3) кв.см
Висота рівнобедреного трикутника є його медіаною і бісектрисою.
Бічні грані правильної піраміди - рівнобедрені трикутники.
За теоремою Піфагора висоти кожного з трикутників SAB, SBC, SAC за теоремою Піфагора дорівнює корінь (SA^2-(AB/2)^2)=корінь(15^2-(18/2)^2)=12 cм
Площа бічної поверхні дорівнює сумі площ бічних граней. (В правильної піраміди вони рівні - і вище згадані рівнобедрені трикутники)
Площа трикутника дорівнює півдобутку основи на висоту, проведену до неї.
Площа бічної грані піраміди дорівнює 3* 1/2*18*12=324 кв.см
Площа повної поверхні=площа бічної+площа основи
Площа повної поверхні = 324+81*корінь(3) кв.см