3600дм² необходимо ткани
4500дм² считая затраты на швы и обрезки.
Объяснение:
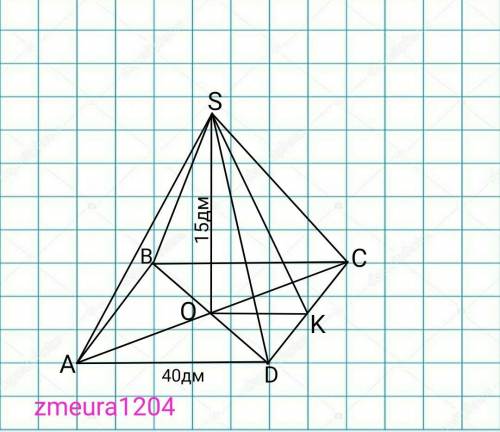
Дано:
SABCD- пирамида
ABCD- квадрат
АВ=ВС=СD=AD=40дм.
SO=15дм.
Sпол=?
Решение
ОК=1/2*АD=1/2*40=20дм проекция апофемы на плоскость.
∆SOK- прямоугольный треугольник
По теореме Пифагора
SK=√(SO²+OK²)=√(15²+20²)=√(225+400)=
=√625=25 дм апофема пирамиды.
Росн=4*АВ=4*40=160дм периметр квадрата.
Sбок=1/2*Росн*SK=1/2*160*25=2000 дм² площадь боковой поверхности пирамиды.
S(ABCD)=AB²=40²=1600дм² площадь квадрата.
Sпол=2000+1600=3600 дм ткани необходимо для пошива палатки.
25%=0,25
3600*0,25=900дм² на швы и обрезки.
900+3600=4500 дм² на пошив палатки считая расходы на швы и обрезки
1
Объяснение:
Для решения данной задачи примем катеты за неизвестные. Пусть они равны a и b соответственно. Тогда согласно условиям задачи составим систему уравнений и решим ее, вычтя из первого уравнения второе:
система выражений a в степени 2 плюс b в степени 2 =49,(a минус 4) в степени 2 плюс b в степени 2 =25 конец системы . равносильно система выражений a в степени 2 плюс b в степени 2 =49, 8a=40 конец системы . \underset{b больше 0}{\mathop{ равносильно }} система выражений a=5,b=2 корень из 6 . конец системы .
Таким образом, первоначально горка была высотой 5 м и длиной 2 корень из 6 \approx 4,9 м. После уменьшения горки, ее параметры стали равны 1 м и 4,9 м соответственно.
Подставляя 2<АВД/3+<АВД=90, получим <АВД=90*3:5=54, тогда <СВД=36.
Из треугольника АВД находим <АДВ=180-90-<АВД=36.
Диагонали прямоугольника АС и ВД равны и в точке пересечения О делятся пополам ( АО=ОД=ВО=ОС), значит треугольник АОД равнобедренный и углы при основании равны <АДВ=<ДАС=36. Тогда <АОД=180-2*36=108 градусов.