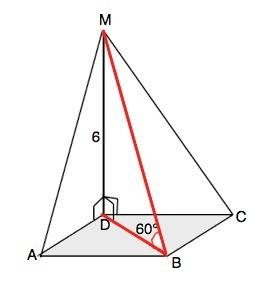
а) По условию MD перпендикулярна плоскости квадрата,
АD -проекция АМ на плоскость квадрата.
СD - проекция СМ на плоскость квадрата.
По т. о 3-х перпендикулярах МА⊥АВ, и МС⊥СВ.
Углы МАВ и МСВ прямые,⇒ ∆ МАВ и Δ МСВ прямоугольные.
б) В прямоугольном ∆ МDB катет DB равен MD:tg60°=6:√3=2√3
BD- гипотенуза прямоугольного равнобедренного ∆ ABD, его острые углы=45°.
АВ=ВD•sin45°=2√3•√2/2=√6
в) МD перпендикулярна плоскости квадрата по условию.
В ∆ АВD катет АD является проекцией наклонной АМ на плоскость квадрата.
Гипотенуза DB является проекцией МВ на плоскость квадрата.
АВ - общий катет ∆ АМВ и ΔΔ ADB. ⇒ ∆ ABD является проекцией ∆ MAB на плоскость квадрата.
в) В ∆ МАВ по т. о 3-х перпендикулярах наклонная МА⊥АВ,⇒
∆ МАВ прямоугольный.
Ѕ=AM•AB:2
Из ∆ АМD по т.Пифагора АМ=√(MD²²+AD²²)=√(36+6)=√42
S=√42•√6=√(7•6•6)=6√7 см²
№2
найдем координаты вектора АВ: АВ = (15; -5)
из отношения АВ:ВС = 5:1, следует, что АС: АВ = 6:5
вектор АС = вектор АВ* 6/5 = (18; -6)
зная координаты вектора АС и координаты его начала находим координаты его конца, то бишь координаты точки С:
С=(18-10;-6+4) = (8;-2)
№3
соsα = (3*5 + 4*12)/(√(3²+4²)*√(5² +12²²)) = 63/65
№4
в общем для доказательства нужно знать суммирование векторов по правилу параллелограмма
достраиваешь треугольник до параллелограмма, продолжаешь медиану на ее собственную длину и получается диагональ параллелограмма, а дальше все будет видно