1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение.
Треугольники HOBи KOB равны, т. к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=3
PABC=AC+CB+AH+HB=2CB+2HB=16+6=22
ответ: 22
2. В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус окружности, если АМ = 8 и ВМ = 12.
S=1/2p*r
r=2s/p
Т.к треугольник ABC-равнобедренный, то AB=AC=30
По свойству касательных: АМ=АЕ=8, СЕ=СК=12,ВМ=КВ=12,значит ВС=24
По формуле Герона S треугольник = в корне p(p-a)(p-b)(p-c)
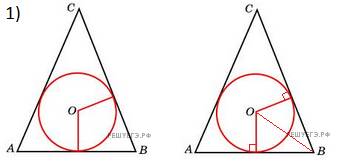
сделаем построение по условию
дополнительные построения
OO1 перепендикуляр к CD
DO1=CO1=DC/2=AB/2=4/2=2
В1К:КС1=3:1
KC1=1
прямая О1С1 - ортогональная проекция прямой ОК на плоскость CDD1
точка К1 - пересечение прямой ОК1 и её проекции О1С1
искомый угол < φ = < ОК1О1
∆O1CC1 - прямоугольный
по теореме Пифагора
O1C1=√(2^2+2^2)=2√2
∆OO1K1 ~ ∆KC1K1 подобные по двум углам <90 ; <φ
обозначим C1K1=a
тогда
OO1/KC1 =O1K1/K1C1
2/1=(2√2+a)/a
a=2√2
tg<φ=KC1/K1C1=1/2√2=√2/4
ответ <φ = arctg 1/2√2 = arctg √2/4