Толя, миша, и никита покупали сливы. миша купил на 20 % меньше, чем толя,а никита на 10% меньше, чем миша. на сколько процентов больше слив купил толя, чем миша

👇

Ответ:

ghjAlina11181

28.01.2021

Краткая запись:
Толя - 0,2 + х
Миша - х
Никита - х - 0,1
(Чтобы перевести процент в число, нужно разделить на 100)
0,2 + х + х + х - 0,1 = 1
(Равно одному, т. к. всего было 100%, а 100 разделить на 100 будет 1)
3х = 0,9
х = 0,9 : 3
х = 0,3
0,3%(30%) - слив купил Миша.
0,3 + 0,2 = 0,5%(50%) - слив купил Толя.
0,5 - 0,3 = 0,2%(20%) слив больше купил Толя.
ответ: на 20%.

4,4(55 оценок)

Открыть все ответы

Ответ:

olesya12let

28.01.2021

Для того чтобы число делилось на 9, необходимо и достаточно чтобы сумма всех его цифр при делении на 9 давала в остатке 0. Соответственно второй игрок (всегда делающий последний ход) будет стремиться добиться нуля в остатке.
Рассмотрим варианты игры второго игрока и позиции, которые он может гарантировано занять за определённое число ходов.
Можно заметить, что своим первым ходом (т.е после того как напишет 2-ую цифру числа), второй игрок может гарантировано добиться остатка 6 (при делении на 9). (Т.к. если первый игрок напишет цифру 1, второй напишет 5, если первый напишет 2, то второй - 4, ..., если первый игрок напишет цифру 5, то второй - 1). Если своим первым ходом второй игрок сможет получить в остатке 6, то своим вторым ходом сможет гарантировано получить в остатке 3, по тому же принципу. И наконец своим третьим ходом (написав 6-ую цифру числа), второй игрок гарантировано получит в остатке 0. Далее - после своего четвёртого хода, второй игрок опять сможет получить в остатке 6, потом снова 3, потом 0 и т.д.
Следовательно второй игрок может получить в остатке 0 не только на своём третьем ходе (написав 6-ую цифру числа), но и на шестом, на девятом, на двенадцатом, ..., на 3n-ом ходе (написав соответственно 12-ую, 18-ую, 24-ую, ..., 6n-ую цифру числа). n ∈ N.
Из этого можно сделать вывод, что второй игрок сможет гарантировано достичь того, чтобы полученное число делилось на 9 тогда и только тогда, когда в этом числе будет 6n цифр. Это значит, что если школьники пишут цифры 2k-значного числа, второй школьник выиграет, только в том случае когда k будет делиться на 3. (тогда 2k будет делиться на 6) (при правильной игре).
Конкретно когда k = 10, второму школьнику не удастся выиграть, т.к. 10 не делится на 3. В том случае когда k = 15, победит второй школьник.
ответ: второй школьник одержит победу если k кратно 3. При k = 10 победит первый школьник (игрок), при k = 15 - второй.

4,4(56 оценок)

Ответ:

gamer0072

28.01.2021

Случай 1. Биссектриса проведена из вершины тупого угла трапеции.

У трапеции, описанной около окружности, сумма боковых сторон равна сумме оснований.

Боковая сторона для равнобокой трапеции АВСД равна:

АВ = (4+16)/2 = 20/2 = 10.

Высота Н трапеции равна:

Н = √(10²-(16-4)/2)²) = √(100-36) = √64 = 8.

Площадь S трапеции равна:

S = ((4+16)/2)*8 = 10*8 = 80.

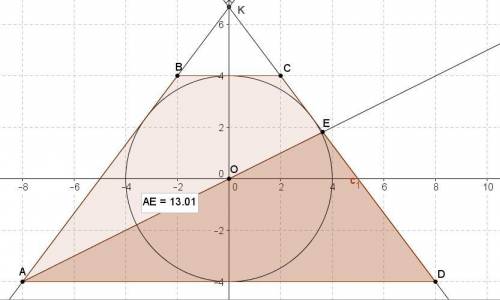
Так как центр О окружности находится на середине высоты, проходящей через точку О, то точка Е находится на основании АД на расстоянии от высоты, равном половине верхнего основания.

Площадь треугольника АВЕ, отсекаемого от трапеции биссектрисой ВЕ, равна (1/2)*8*((16/2)+(4/2)) = 4*10 = 40.

Отношение равно 40/80 = 1/2.

2 случай - биссектриса АЕ проходит через вершину острого угла.

Продлим боковые стороны трапеции до пересечения в точке К.

Биссектриса АЕ будет и биссектрисой треугольника АКД.

Отрезок ВК находим из подобия треугольников:

ВК/(ВС/2) = АВ/6. ВК = 2*10/6 = 10/3.

Сторона АК = 10 + (10/3) = 40/3.

Находим биссектрису АЕ. Но сначала находим косинус половины угла А.

AO = √(8² + 4²) = √)64 + 16) = √80 = 4√5.

cos (A/2) = 8/(4√5) = 2/√5 = 2√5/5.

Тогда АЕ = (2ab/(a+b))*cos(A/2) = (2*(40/3)*16)/((40/3)+16)*(2/√5) = (1280/88)*(2√5/5) = 64√5/11.