Задайте вектор m , начало и конец которого лежат в вершинах тетраэдра АВСD и выполняется следующее условие вектор
АС=АВ-m-СD
Объяснение:
Векторам присущи свойства которые позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым :
АС=АВ-m-СD,
m=АВ-СD-АС,
m=АВ-АС-СD . По правилу вычитания векторов (оба вектора выходят из общей точки А , стрелка разности к уменьшаемому) АВ-АС =СВ;
m=СВ-СD , и снова правило вычитание векторов , тк они выходят из общей точки С ,
m=DВ.
В таких задачах даже чертеж не нужен.
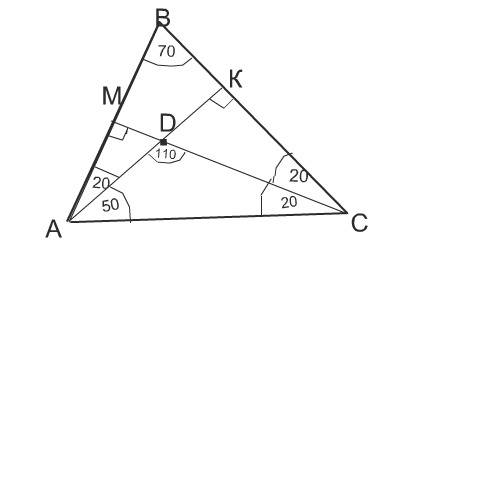
Нарисуем треугольник АВС.
Проведем в нем высоты АК и СМ.
По условию задачи они пересекаются под углом 110º.
1) Рассмотрим треугольник АМС.
Угол АМС =90º
Сумма острых углов в нем 90º, ∠А=70º по условию, следовательно,
∠ МСА=90º-70º=20º.
2)Рассмотрим треугольник АDС.
Так как ∠МСА=20 градусов,
то ∠DAC=180-110-20=50º.
3)Так как ∠ А=70º, а
∠КАС=50º,то ∠ВАК=70-50-20º
4)В прямоугольном треугольнике АВК ∠АКВ прямой, ∠ВАК=20º, следовательно, ∠В=90-20=70º
5) В треугольнике АВС ∠С=180-70-70=40º
ответ: Угол С=40º
Объяснение:π
Осевое сечение цилиндра - прямоугольник со сторонами h и 2r
Его площадь:
S=2r*h=2*50*80= 8000 cм^2
Площадь полной поверхности = Площадь боковой поверхности + 2*Площадь основания
Площадь боковой поверхности
S=2πrh=2*π*50*80=8000π (см^2)=80π(дм^2)
Площадь основания
S=π*r^2=π*50^2=2500π=25π (дм^2)
Площадь полной поверхности
S=8000π+2*2500π=13000π (см^2)=130 (дм^2)
Объем:
V=π*r^2*h=π*50^2*80=200000π (см^3)= 200 (дм^3)