ответ:Геометрический смысл φ ясен из рис. 125. Отрезок прямой разделен на два отрезка А и В, которые, как говорят, образуют "золотое сечение" отрезка А + В: длина всего отрезка (А + В) находится в таком же отношении к длине отрезка А, как и длина отрезка А к длине отрезка В. Отношение каждой пары отрезков и равно числу φ. Если длина отрезка В равна 1, то значение φ нетрудно вычислить из уравнения
которое можно записать в виде обычного квадратного уравнения А2 - А - 1 = 0. Положительный корень этого уравнения равен
Это число одновременно выражает длину отрезка А и значение величины φ. Его десятичное разложение имеет вид 1,61803398... Если за единицу принять длину А, то длина В будет выражаться величиной, обратной φ, то есть 1/φ. Любопытно, что 1/φ = 0,61803398... Число φ - единственное положительное число, которое переходит в обратное ему при вычитании единицы.
Подобно числу π, φ можно представить в виде суммы бесконечного ряда многими Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер φ:
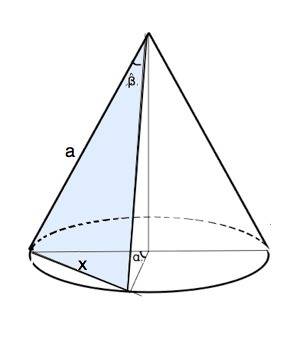
Через вершину конуса с основанием радиуса R проведена плоскость, которая пересекает его основание по хорде, которую видно из центра основания под углом α, а из вершины – под углом β. Найти площадь сечения.
--------
Данное сечение конуса - равнобедренный треугольник. Пусть сторона этого треугольника равна а.
Тогда его площадь можно выразить S=a²•sinβ/2.
1) Примем длину хорды равной х. Тогда из треугольника в основании, образованного хордой и двумя радиусами, квадрат её длины можно выразить по т.косинусов.
х²=2R²-2R²•cosα=2R²(1-cosα)
2) Выразим квадрат длины хорды по т.косинусов из треугольника в сечении:
х²=2а²-2а²•cosβ=2а²(1-cosβ)
3) Приравняем найденные значения х²
2R²(1-cosα)=2а²(1•cosβ)
Выразим а² из этого уравнения:
а²=R²(1-cosα):(1-cosβ)
Отсюда
S сечения=[R²(1-cosα):(1-cosβ)]•sinβ:2
Высота ОD тетраэдра равна √(2/3). Основание высоты - точка О.
Для нахождения угла между скрещивающимися прямыми надо одну из прямых параллельно переместить до образования угла в одной плоскости.
Отрезок DM находится на апофеме боковой грани.Обозначим её основание буквой Е
Из этой точки проводим отрезок ЕР параллельно АК, По длине ЕР равен 2/3 АК (свойство медиан правильного треугольника).
В плоскости основания получаем треугольник РОЕ, который является проекцией искомого угла.
В этом треугольнике известны две стороны РЕ и ЕО и угол между ними, равный 120°. Сторона РЕ равна 2/3 от АК.
Высота АК в равностороннем треугольнике равна √3/2, поэтому РЕ = (2*√3) / (3*2) = √3/3, а ЕО = (1/3) АК = (1*√3) / (3*2) = √3/6.
Сторону РО находим по теореме косинусов: РО = √(РЕ²+ОЕ²-2РE*ОЕ*cos E) = √((√3/3)²+(√3/6)²-2*(√3/3)*(√3/6)*(-1/2)) =
√21/6.
Теперь переходим к треугольнику РОD для нахождения неизвестной стороны PD = √(РО²+ОD²) = √((√21/6)²+(√(2/3))²) = √5/2.
Апофема DЕ равна АК, поэтому в треугольнике PDE известны 3 стороны, искомый угол PED находим по теореме косинусов:
cos PED = (PE²+ED²-PD²) / (2*PE*ED) = ((3/9)²+(3/4)²-(5/4)) / (2*(√3/3)*(√3/2) = -1/6.
Такому косинусу соответствует угол 1.738244 радиан или 99.59407°.