Объяснение:
Очевидно, что внутри отрезка AB такой точки существовать не может (если бы существовало, тогда сумма двух меньших отрезков должна быть больше длины исходной, что является противоречием), поэтому эта точка должна лежать где-то за пределами отрезка (по условию же сказано, что нужно найти точки на прямой, а не внутри отрезка).
Пусть l - расстояние от искомой точки X до A, тогда l + 6 - это расстояние от X до B. Тогда справедливо уравнение:
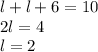
Значит, точка X должна отстоять от точки A на 2 см
Выглядит схематично это так:
2см 6см
---------------|----------------|------------------------------------------|----------------->
X A B
Это справедливо и для случая:
6см 2см
------------------|------------------------------------------|-------------|--------->
A B X
Больше таких точек нет.
Объяснение:
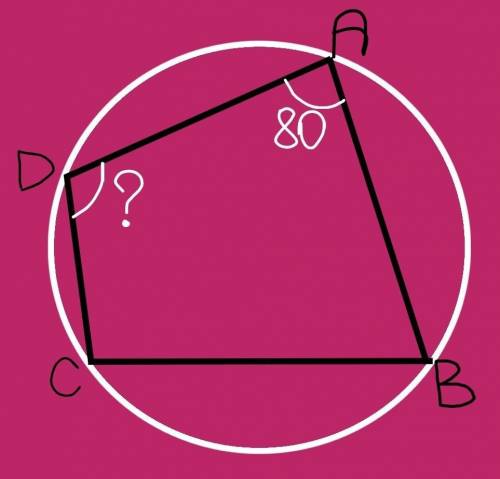
№1 фото
Условие некорректно! Скорее всего надо было найти угол С.
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Углу А противоположен угол С, тогда угол С=180°–угол А=180°–80°=100°.
ответ: б) 100°
Найти угол D, незная угол В или не имея других данных, невозможно.
№2
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Тогда угол CDA=180°–угол АВС=180°–110°=70°.
Сумма углов в любом треугольнике равна 180°.
Следовательно угол ACD=180°–угол CAD–угол CDA=180°–50°–70°=60°
ответ: в) 60°
№3
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны.
Тоесть ВС+AD=AB+CD
Пусть АВ=4n, тогда CD=3n.
Подставим значения в уравнение:
13+22=4n+3n
35=7n
n=5
Тогда CD=3*5=15 см
ответ: а) 15 см.