Надо ответить верно или не верно 1) если прямые не пересекаются, то они параллельны? 2) если две плоскости не параллельны, то они пересекаются? 3) две прямые прямые называются перпендикулярными, если угол между ними равен 90 градусов? 4) две плоскости не имеющие общих точек параллельны? 5) две прямые скрещиваются, если они имеют общую точку? 6) две плоскости называются перпендикулярными, если они пересекаются под углом 90 градусов? 7) две прямые называются параллельными, если они не скрещиваются 8) две плоскости называются параллельными, если они не пересекаются 9) две прямые называются скрещивающимися, если он не параллельны 10) две плоскости не имеющие общих точек 11) две прямые называются параллельными, если они не имеют общих точек 12) две плоскости называются параллельными, если угол между ними не равен 90 градусов 13) две прямые называются скрещивающимися, если угол между ними равен 90 градусов 14) две плоскости , если они имеют общую точку

👇

Увидеть ответ

Ответ:

diyoyoroo

14.10.2021

1-9, 11 и 14 - верно, 12 и 13 - неверно, 10 не дописано.

4,5(13 оценок)

Открыть все ответы

Ответ:

natashasheh

14.10.2021

Так как AK - биссектриса, то:
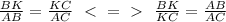
$\frac{BK}{AB}= \frac{KC}{AC} \ \ \textless \ =\ \textgreater \ \ \frac{BK}{KC}= \frac{AB}{AC}$
при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки:
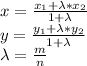
$x= \frac{x_1+\lambda*x_2}{1+\lambda} \\y= \frac{y_1+\lambda*y_2}{1+\lambda} \\\lambda= \frac{m}{n}$
ищем длины AB и AC:
используем формулу:
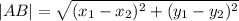
$|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
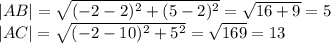
$|AB|=\sqrt{(-2-2)^2+(5-2)^2}=\sqrt{16+9}=5 \\|AC|=\sqrt{(-2-10)^2+5^2}=\sqrt{169}=13$
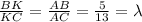
$\frac{BK}{KC}= \frac{AB}{AC}= \frac{5}{13} =\lambda$
находим координаты точки K:
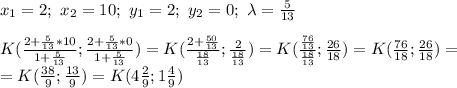
$x_1=2;\ x_2=10;\ y_1=2;\ y_2=0;\ \lambda=\frac{5}{13} \\ \\K( \frac{2+ \frac{5}{13}*10 }{1+\frac{5}{13}} ;\frac{2+ \frac{5}{13}*0 }{1+\frac{5}{13}})=K( \frac{2+ \frac{50}{13} }{ \frac{18}{13}}; \frac{2}{ \frac{18}{13} })=K( \frac{ \frac{76}{13} }{ \frac{18}{13}}; \frac{26}{18} )=K( \frac{76}{18}; \frac{26}{18}) = \\=K( \frac{38}{9}; \frac{13}{9})=K(4 \frac{2}{9};1 \frac{4}{9} )$
теперь определим вид треугольника для этого используем теорему косинусов:
для начала найдем длину BC:
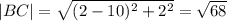
$|BC|=\sqrt{(2-10)^2+2^2}=\sqrt{68}$
вид треугольника будем определять по косинусу самого большого угла; если cos<0, то угол тупой; если cos=0, то угол прямой; если cos>0, то угол острый.
Против большей стороны лежит больший угол, поэтому запишем теорему косинусов для AC и косинуса угла B
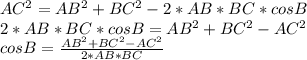
$AC^2=AB^2+BC^2-2*AB*BC*cosB \\2*AB*BC*cosB=AB^2+BC^2-AC^2 \\cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}$
подставим значения:
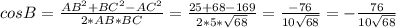
$cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}= \frac{25+68-169}{2*5*\sqrt{68}}= \frac{-76}{10\sqrt{68}} =- \frac{76}{10\sqrt{68}}$
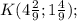cosB<0 поэтому угол тупой и треугольник тупоугольный
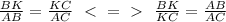
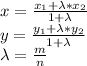
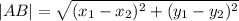
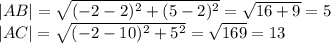
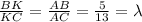
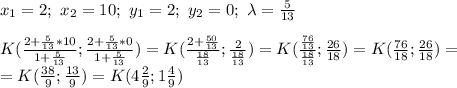
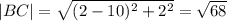
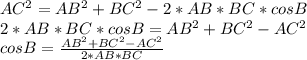
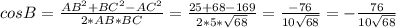
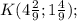ответ: $K(4 \frac{2}{9};1 \frac{4}{9} );\$ треугольник тупоугольный