Дано:
AD-BC=8см
AB+CD=10см
sin a-?
cos a-?
tg a-?
Решение
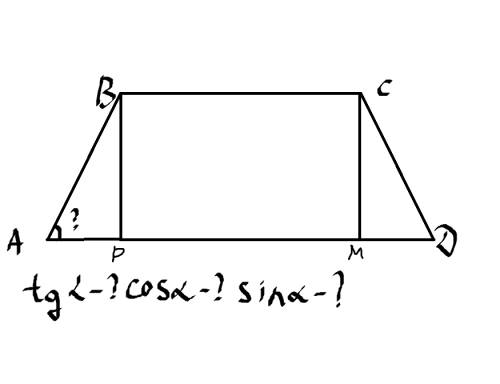
1) Проведем перпиндекуляры из углов B и C к основанию AD
2) Т.к. по условию AD-BC=8 см, то AP+MD+PM-BC=8 см
3) Рассмотрим треугольники ABP и CMD. Они равны по 1 признаку:
1) BP=CM (как перпендикуляры проведенные из равных по величине углов)
2) угол A=D (как углы при основании равнобедренной трапеции)
3) AB=CD (как стороны равнобедренной трапеции)
4) Т.к. треугольники ABP и CMD равны, то AP=MD. Т.к. BC=PM, AP=MD то
AP+MD+PM-BC=8 см
2AP=8 см
AP=4 см
5) AB+CD=10 см - по условию
Т.к. стороны равнобедренной трапеции равны, то
2AB=10 см
AB=5 см, следовательно и CD=5 см
6) Т.к. AB=5 см, AP=4 см, то по теореме Пифагора:
BP=корень (AB^2-AP^2)=корень (25-16)=3 см
7) sin a= BP\AB=3\5=0,6 (синус-отношение противолеж. катета к гипотенузе)
cos a= AP\AB=4\5=0,8 (косинус-отношение прилежащего катета к гипотеннузе)
tg a= BP\AP=0,75 (тангенс-отношение противолеж. катета к прилежащему)
ответ: sin a=0,6 ;cos a=0,8 ;tg a=0,75.
Рассмотрим горизонтальную проекцию пирамиды. Пирамида правильная значит в основании правильный треугольник со стороной 4, и в сечении также правильный треуголник со стороной 1. Построим равносторонний треугольник АВС со стороной 4, затем в центре его параллельно сторонам первого треугольника построим треугольник MFN со стороной 1. Проведём боковые рёбра пирамиды АМ, BF,CN. Проведём высоту большего основания ВД. Отметим на ней точку О центр вписанной окружности. В неё проецируется вершина пирамиды О1. Причём , в правильном треугольнике ДО=1/3ВД=1/3*(( корень из( 16-4))=1,15. Боковая грань АМNC равнобедренная трапеция . Проведём в ней высоту NQ=КД=корень из (4-1,5)=1,32(по теореме Пифагора). Точка К расположена на пересечении MN и ВД. В плоскости перпендикулярной АВС и проходящей через ВД получим трапецию ДКFB. Точка О лежит на ДВ. Восстановим из неё перпендикуляр до пересечения с продолжением АК в точке О1. ДО1=1,76 найдём из подобия треугольников. Из точки К опустим перпендикуляр KG на ДВ. cos О1ДО=ДО/ДО1=0,653. Отсюда sin О1ДО=0,764.Тогда Н=KG=КД*sin О1ДО=1,32*0, 764=1,0.
1) Пусть в многоугольнике n сторон.
Сумма углов выпуклого n -угольника равна
180°·(n-2)
Но и углов в многоугольнике тоже n, поэтому сумма всех углов равна
150°·n
Приравниваем выражения и получаем уравнение:
180·(n-2) = 150·n
180·n - 360 = 150·n
180·n - 150·n = 360
30·n = 360
n= 12
ответ. 12 сторон.
2) Гипотенуза = корень (катет1 в квадрате + катет2 в квадрате) =
=корень(400+441)=29 =диаметру описанной окружности
радиус = 29/2 =14,5
3) так как правильный четырехугольник - это квадрат, то радиус будет равен половине диагонали квадрата, то есть
a=16/4=4 (сторона квадрата)
d^2=(a^2+a^2) (диагональ)
d=корень из 32=4 умножить на корень из 2
r=2 умножить на корень из 2
4) Диаметр окружности равен стороне квадрата, то есть 8 см, значит радиус окружности 4 см, 2/3 высоты вписанного правильного треугольника равны радиусу окружности
2/3h=4. значит h=6 cм , а h в правильном треугольнике равна а√3/2, где а- сторона правильного треугольника значит
а=2h/√3=2*6/√3=4√3