ответ: 52,3м; 104,6м
Объяснение:
Сам монумент, расстояние от точки А до основания монумента и расстояние от точки А до самой высокой точки образуют прямоугольный треугольник.
Высота монумента является катетом, расстояние от основания до точки А вторым катетом, а расстояние от точки А до вершины монумента гипотенузой.
Для того чтобы найти расстояние от точки А до вершины, нужно выстоу монумента разделить на sin60° и получим:
91/0,87=104,6м
Для нахождения расстояния от основания монумета до точки А, нужно расстояние от точки А до самой высокой точки умножить на cos60°: 104,6*0,5=52,3м
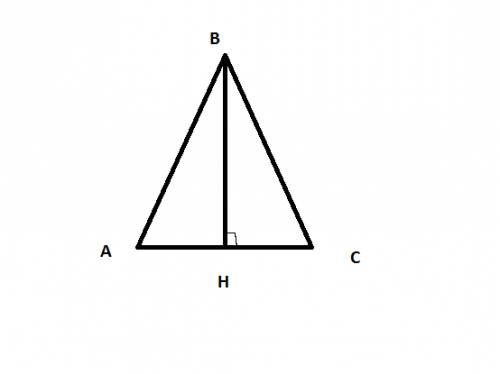
1) Проведем высоту из вершины равнобедренного треугольника, по его свойствам она будет медианой, следовательно разделит основания на равные отрезки по 8. В прямоугольном трегольники ABH, по теореме Пифагора следует BH^2=AB^2-AH^2
BH^2=289-64; BH=15,
S=AC*BH/2
S=15*16/2=120 см^2
2) Диагонали ромба относятся как 4 : 5, а его площадь равна 40 см2. Найдите диагонали ромба. Наверное так..?
d1/d2=4/5, 4d1=5d2, d1=5d2/4, d1=1,25d2
Пусть первая диагональ это x, тогда вторая 1.25x, подставим в формулу площади ромба S=d1*d2/2
S=x*1.25x/2, 40=1.25x^2/2, решив уравнение получим x=8, значит вторая диагональ равна d2=1.25* 8=10
ответ: 8 см и 10 см
б) 10√3-4√48-√75=10√3-4*√(4²*3)-√(5²*3)=√3(10-16-5)=-11√3