Прямая параллельная стороне ab треугольника abc пересекает стороны ас и вс в точках м и n соответственно - id329440220210907 от horarharry 07.09.2021 05:29

Question

Геометрия: Прямая параллельная стороне ab треугольника abc пересекает стороны ас и вс в точках м и n соответственно . найдите ас если см= 14 см, сn=18, вс=27 см варианты 20,21,22,22.5

horarharry · Accepted Answer

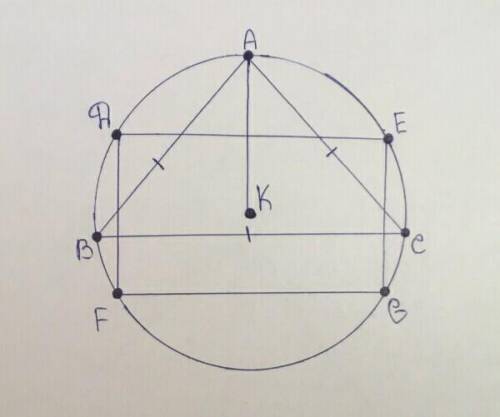
Пусть дана окружность с центром в точке K, равносторонний треугольник ABC и вписанный квадрат DEFG.

Периметр треугольника это сумма всех длин его сторон.

Т.к. треугольник ABC - равносторонний, то AB=BC=AC=18/3=6 (см).

Проведём из точки B равностороннего треугольника АВС отрезок к центру окружности в точке К так, что отрезок АК - радиус данной окружности.

Вспомним формулу радиуса равностороннего треугольника: R=a:√3.

=> радиус равностороннего треугольника АВС=6:√3=(6√3)/3=2√3 (см).

Вспомним формулу стороны описанного квадрата: a=R√2.

=> сторона вписанного квадрата DEFG=2√3*√2=2√(3*2)=2√6 (см).

В квадрате все стороны между собой равны.

=> DE=EG=GF=FD=2√6 (см).

ответ: сторона DE вписанного квадрата DEFG равна 2√6 (см).

Периметр правильного треугольника, вписанного в окружность, равен 18 см. Найдите периметр квадрата,

Прямая параллельная стороне ab треугольника abc пересекает стороны ас и вс в точках м и n соответственно . найдите ас если см= 14 см, сn=18, вс=27 см варианты 20,21,22,22.5

MOGZ ответил