3) Чтобы найти AK, нужно найти MK.
MK=MD-AC,=9-5=4см.
Найдём AK за теоремой Пифагора, тоесть AK²=AM²-MK²
AK²=20-16=4см, AK=2см.
4) Пускай BC-x, тогда AC-x+3.
x²+(x+3)²=29, за теоремой Пифагора
x²+x²+6x+9=29
2x²+6x+9-29=0
2x²+6x-20=0
x²+3x-10=0
x²+5x-2x-10=0
x(x+5)-2(x+5)=0
(x-2)(x+5)=0
x-2=0, x+5=0
x=2, x=-5, но x>0, поэтому BC=2, AC=2+3=5.
5)Косинус-отношение прилежаещего катета к гипотенузе, тоесть cosB=a/c=6/10=0,6.
Тангенс-отношение протилежащего катета к прилежащему, тоесть tgA=b/a=8/6=4/3.
6)AH-сторона напротив угла 30°, поэтому равна половине гипотенузы, тоесть 14:2=7.
HC²=AC²-AH²,
HC²=196-49,
HC²=147,
HC=7√3.
∆ABH-равнобедренный, т.к. <BAH=45°, <ABH=180-90-45=45°, тогда BH=AH=7см.
AB²=BH²+AH²,
AB²=49+49,
AB²=98,
AB=7√2.
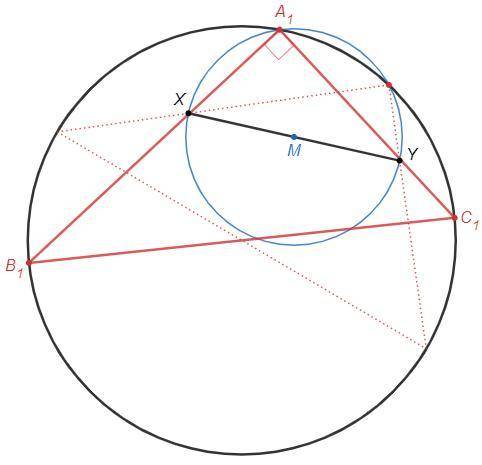
Дана окружность и точки X и Y внутри нее.
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.
1.Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
s=((a+b)/2)*h
88=((5x+6x)/2)*4x
находим х=2
соответственно меньшее основание 5х=5*2=10
2. После нахождения высоты и оснований, находим площадь треугольника ACD по формуле s=(1/2a)*h. Тогда площадь треугольника ABC будет равна площадь трапеции минус площадь треугольника ACD.