1. На данной прямой а отметим произвольную точку А.
2. Проведем окружность произвольного радиуса с центром в точке А. Точки пересечения окружности с прямой а обозначим В и С.
3. Проведем две окружности одинакового произвольного радиуса (большего половины отрезка ВС), с центрами в точках В и С.
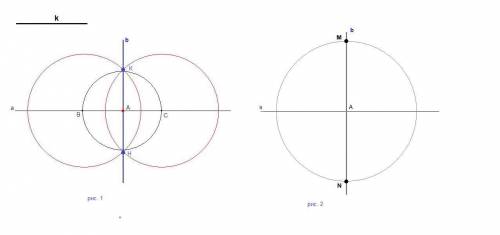
4. Через точки пересечения этих окружностей (К и Н) проведем прямую b.
Прямая b - искомый перпендикуляр к прямой а. (см. рис. 1)
5. Проведем окружность с центром в точке А с радиусом, равным данному отрезку k. Точки пересечения этой окружности с прямой b обозначим M и N. (см. рис. 2)
Точки М и N - точки, удаленные от точки пересечения прямых на расстояние, равное длине данного отрезка.
Все построение надо выполнять, конечно, на одном чертеже. Для наглядности построение последнего пункта выполнено отдельно.
копирую
Радиус сечения шара и расстояние от центра шара до плоскости сечения связаня с радиусом шара теоремой Пифагора
r^2 + d^2 = R^2; В данном случае, поскольку тройка 3,4,5 - пифагрова, расстояния до сечений равны d1 = 4; - до сечения радиуса r1 = 3; соответственно, высота шарового сегмета, ОТРЕЗАННОГО от шара, равна H1 = R - d1 = 5 - 4 = 1; и d2 = 3; для r2 = 4; соответственно Н2 = R - d2 = 5 - 3 = 2;
Поскольку сечения находятся по разные стороны от центра, для получения объема пояса надо из объема шара вычесть объемы шаровых сегментов высоты H1 и H2.
(Если бы они были по одну сторону - надо было бы из объема большего сегмента вычесть меньший.)
Итак, объем шара
V0 = (4*pi/3)*5^3 = 500*pi/3;
Объем первого сегмента высоты Н1 = 1
V1 = pi*1^2*(5 - 1/3) = 14*pi/3;
b второго высоты Н2
V2 = pi*2^2*(5 - 2/3) = 52*pi/3;
Объем пояса
V3 = (pi/3)*(500 - 14 - 52) = 434*pi/3
3)12^2+5^2=169=13 см