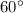Теорема 1. Шар можно вписать в прямую призму в том и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.
Следствие 1. Центр шара, вписанного в прямую призму, лежит в середине высоты призмы, проходящей через центр окружности, вписанной в основание.
Следствие 2. Шар, в частности, можно вписать в прямые: треугольную, правильную, четырехугольную (у которой суммы противоположных сторон основания равны между собой) при условии Н = 2r, где Н – высота призмы, r – радиус круга, вписанного в основание.
Вывод: радиус сферы, вписанной в прямую призму высота которой равна h, равен половине этой высоты.
На координатной плоскости есть окружность радиусом √2/2, с центром в начале координат. На отрезке, диаметре этой окружности, с концами А (0, √2/2) и В (0,-√2/2) построен равносторонний треугольник АВС1.
Его третья вершина лежит в точке С1 (√6/2,0).
Окружность с центром в этой точке и радиусом √7, (если есть решение) пересекает первую окружность в двух точках, симметричных относительно оси X. Координаты точки С в верхней полуплоскости (то есть y>0) находятся так.
x^2 + y^2 = 1/2;
(x - √6/2)^2 + y^2 = 7;
Так вот, у этой системы НЕТ решения, потому что
√6/2 + √2/2 < √7;
То есть эти окружности не пересекаются.
Поэтому при любом угле треугольника сумма расстояний от вершин до точки Ферма (то есть наименьшее возможное значение этой суммы) будет МЕНЬШЕ √7.
Не похоже, что я где то ошибся, но все может быть, проверьте.
Теорию точки Ферма (она же точка Торичелли) в треугольниках я тут излагать не стану. Достаточно понимать, что для прямоугольного треугольника она СУЩЕСТВУЕТ и лежит внутри треугольника.
Расстояние от вершины С, лежащей на окружности x^2 + y^2 = 1/2, до точки С1 ОБЯЗАТЕЛЬНО должно равняться заданному в задаче √7.
(Может, в условии другое число, например, гипотенуза √3, или нвр = √5)
Кстати, для прямоугольного треугольника довольно легко из теоремы косинусов получить соотношение
m^2 = c^2*(1 + (√3/2)*sin(2*Ф))
где Ф - острый угол треугольника, с - гипотенуза, m - минимальная сумма расстояний от внутренней точки до вершин треугольника.
Отсюда сразу видно, что при (m/c)^2 = 7/2; sin(2*Ф) >1; чего быть не может.
Отношение (m/c)^2 максимально равно 1 + √3/2 при Ф = 45 градусов, это примерно 1,866, что почти в два раза меньше, чем 7/2
ответ.