Внешним углом треугольника называется угол смежный с каким-либо углом этого треугольника.
Смотри приложение :
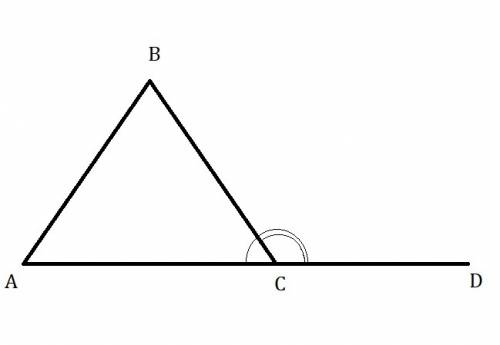
Дан ΔАВС .
При вершине С начертим внешний угол , обозначим его ∠ВСD.
Теорема : Внешний угол треугольника равен сумме двух углов не смежных с ним.
Дано : ΔАВС
Внутренние углы треугольника: ∠ВАС , ∠АВС , ∠ВСА
Внешний угол при вершине С: ∠ВСD
Доказать : ∠ВСD = ∠ВАС + ∠АВС
Доказательство.
1) По теореме о сумме углов треугольника :
Сумма углов (внутренних) треугольника равна 180 градусов.
∠ВАС + ∠АВС + ∠ВСА = 180°
∠ВАС + ∠АВС = 180° - ∠ ВСА
2) По свойству смежных углов:
Сумма смежных углов равна 180 градусов.
∠ВСD + ∠ BCA = 180°
∠ВСD = 180° - ∠BCA
3) ∠ВСD = ∠BAC + ∠АВС = 180° - ∠ВСА
∠ВСD = ∠BAC + ∠ABC , что и требовалось доказать...
СD=AC/2=2/2=1 т.к. DB-медиана(медиана делит сторону пополам)
CB=√DB²+DC²
CB=√4+1=√5
Зная оба катета можно считать гипотенузу треугольника:
АВ=√АС²+СВ²
АВ=√4+5=3
ответ:3