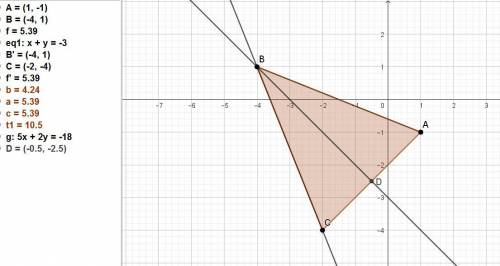
Даны A(1; -1), В(-4; 1) - вершины равнобедренного треугольника, х + у=-3 — биссектриса внутреннего угла между равными сторонами.
Найти уравнение стороны ВС.
Подставим координаты точки В в уравнение биссектрисы.
-4 + 1 = -3. Отсюда видно, что точка В - вершина треугольника при равных боковых сторонах.
Уравнение стороны ВС можно найти двумя путями.
1 - найти точку С как симметричную точке А относительно биссектрисы.
Потом составить уравнение ВС как прямую через 2 точки.
2- найти угол (точнее тангенс угла) между прямой АВ и биссектрисой. Затем определить угловой коэффициент стороны ВС по разности угловых коэффициентов АВ и биссектрисы (свойство симметрии прямых АВ и ВС относительно биссектрисы).
1) Находим к(AD) из уравнения биссектрисы у = -х - 3 .к(BAD) = -1
Уравнение AD: y =( -1/(-1))x + b.Подставим координаты точки A:
-1 =1*1 + b, отсюда b = -1 - 1 = -2. AD: y = x - 2 или х - у - 2 = 0.
Находим координаты точки D, решая систему уравнений BD и AD.
{х + у + 3 = 0
{x - y - 2 = 0
2x + 1 = 0 x = -1/2, y = x - 2 = (-1/2) - 2 = -2,5.
Находим координаты точки С как симметричной точке А относительно точки D.
x(С) = 2x(D) - x(A) = 2*(-1/2) - 1 = -2.
y(С) = 2y(D) - y(A) = 2*(-2,5) - (-1) = -4.
Теперь находим уравнение ВС. Вектор ВС = (-4-(-2); 1-(-4)) = (-2; 5).
(x + 4)/(-2) = (у - 1)/5.
Или в общем виде 5х + 2у + 18 = 0.
$бок=80√3;. V=20√3
Объяснение:
Дано: ∆АВС, а=5; в=16; <с=120
<£=30
Sбок=?;. V=?,
Sбок = $1+$2+$3
V=1/3*$осн*h
По т,косинусов определяем сторону "с",. с^2=а^2+в^2-2авCos120 c^2=5^2+16^2-2*5*16(-0,5)=25+256+80
c^2= 361;. c=√361=19
$осн=1/2*авSinC=1/2*5*16*Sin120
Sосн=40*√3/2=20√3
Двугранный угол 30 градусов => апофема бок.грвни L=2h,. h-высота пирамиды.
Проекция апофем на плоскость ∆ даёт радиус вписанной в основание окружность, , r=S/p
p=(a+в+с)/2=(5+16+19)/2=20
r=20√3/20=√3 (катет против <=30°)
L=2r =2√3 ( гипотенуза)
h= √(L^2 - r^2)=√((2√3)^2-√3^2)=√9=3
Sбок = Росн*L
Sбок= (5+16+19)*2√3=80√3
Vпир= 1/3*$осн*h=1/3*20√3*3=20√3
S=7см*4см=28см^2