Решите, на поверхности шара выбраны точки а и в так, что ав -40см,а расстояние от центра до прямой ав равно 15см.найдитте площадь сечения шара ,проведенного через точки ав на растоянии 7 см от центра шара

👇

Ответ:

antongrom68

03.01.2021

На поверхности шара выбраны точки А и В так, что АВ - 40 см, а расстояние от центра до прямой АВ равно 15см. Найдите площадь сечения шара , проведенного через точки АВ на растоянии 7 см от центра шара.
***
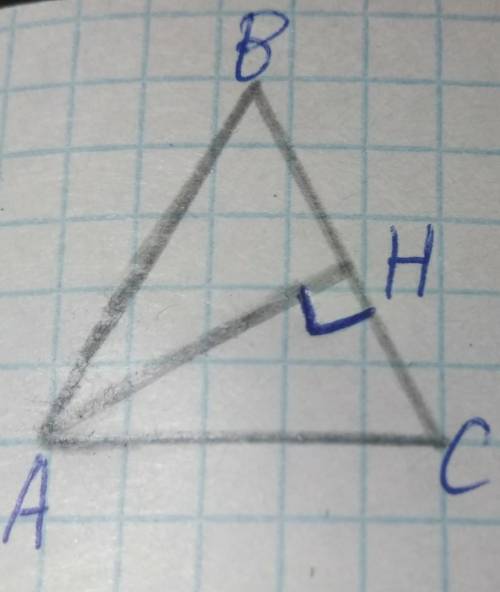
Расстояние от центра О шара до прямой, проведенной в нем, это перпендикуляр из центра шара к этой прямой.
Через прямую и точку, не лежащую на ней, можно провести плоскость. (рис.1 приложения)
Плоскость, проведенная через центр круга и АВ отсекает от шара окружность, в которой АВ - хорда, расстояние из центра О до АВ - перпендикуляр ОН, который, по свойству радиуса, делит АВ пополам.
Треугольник АНО - прямоугольный с катетами АН=(40:2) см и НО=15см, и гипотенузой АО=R.
АО=√(400+225)=√625=25 см
Радиус шара равен 25 см.
Центр сечения, отстоящено от центра шара на расстоянии 7 см, это точка М. Через М и АВ можно провести плоскость, которая является окружностью с радиусом МС. (рис.2 приложения)
ОМС - прямоугольный треугольник с катетами МО и МС и гипотенузой ОС=R
Треугольник ОМС из Пифагоровых троек с отношением сторон 7:24:25 ( отношение катета и гипотенузы 7:25, значит, второй катет равен 24). Можно проверить по т. Пифагора МС=24 см
Площадь сечения с радиусом 24 см вычислим по формуле площади круга:
Ѕ=πr²
Ѕ=π*24²=576 π см²
Решите, на поверхности шара выбраны точки а и в так, что ав -40см,а расстояние от центра до прямой а

Решите, на поверхности шара выбраны точки а и в так, что ав -40см,а расстояние от центра до прямой а

4,5(36 оценок)

Открыть все ответы

Ответ:

nasibovschool

03.01.2021

Пусть длина верхнего основания 2x
найдём стороны треугольника OCD (нам нужны квадраты сторон)
OC² = 5²+x²
OD² = 5²
CD² = 5²+(5-x)² = 25+25-10x+x² = x²-10x+50
и есть такая чудесная формула для длины медианы треугольника по его сторонам
m = 1/2√(2a²+2b²-c²)
или
4m² = 2a²+2b²-c²
Медиана OM = 5
4*25 = 2*(5²+x²) + 2*5² - (x²-10x+50)
100 = 50 + 2x² + 50 - x² + 10x - 50
50 = x² + 10x
x² + 10x - 50 = 0
D = 100+200 = 300
x₁ = (-10-10√3)/2 - отрицательные корни не интересны
x₂ = (-10+10√3)/2 = 5(√3-1)
средняя линия
КМ = 1/2(10-10+10√3)=5√3
угол при основании найдём из треугольника CED
tg∠D = CE/ED = 5/(5-x) = 5/(5+5-5√3) = 1/(2-√3) = (2+√3)/(4-3) = 2+√3
∠D = arctan(2+√3) = 5π/12 = 75°
Готово :)

100 окружность с диаметром ad = 10 касается меньшего основания вс трапеции авсd и пересекает боковые

100 окружность с диаметром ad = 10 касается меньшего основания вс трапеции авсd и пересекает боковые

4,7(20 оценок)

Ответ:

alenavasina20

03.01.2021

рисунок тут лёгкий, смотри. треугольник АВС- равнобедренный, нижнее основание AC=18 см, AB=BC- боковые стороны, угол ABC=120°, высота AH проведена из угла BAC к стороне BC. найти: AH.

Объяснение:

решение: 1) углы A+B+C=180°- по теореме о сумме углов треугольника, углы A+C=180-угол B=60°, углы А=С=30° как углы при основании равнобедренного треугольника

2)Треугольник AHC- прямоугольный так как АН- высота, угол АНС=90°, в прямоугольном треугольнике гипотенуза AC=18 см, а по свойству угла в 30°, катет AH, лежащий напротив гипотенузы, равен половине гипотенузы, то есть AH=9 см.

ответ: 9 см.