Question

Теорема косинусов(формулировка,чертеж, запись каждой стороны через другие стороны и выражение косинуса угла через другие стороны треугольника! надо ; (

Answer 1

Формулировка теоремы косинусов

Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение: 

$a^{2}= b^{2} + c^{2} -2bc*cos \alpha$

Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними.

Доказательство теоремы косинусов

Рассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)

Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD.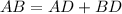 
Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что $AB = AD + BD$

Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике: 

$\frac{AD}{AC} =cos \alpha$

откуда

$AD = AC cos \alpha \\ AD = b cos \alpha$

Длину стороны BD найдем как разность AB и AD:

$BD = AB - AD \\ BD = c-b cos \alpha$

Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:   
для треугольника BDC 

$CD^2 + BD^2 = BC^2$

для треугольника ADC 

$CD^2 + AD^2 = AC^2$

Обратим внимание на то, что оба треугольника имеют общую сторону - CD. Определим ее длину для каждого треугольника - вынесем ее значение в левую часть выражения, а остальное - в правую. 

$CD^2 = BC^2 - BD^2 \\ CD^2 = AC^2 - AD^2$

Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений: 

$BC^2 - BD^2 = AC^2 - AD^2$

Исходя из сделанных ранее вычислений, мы уже знаем что: 

$AD = b cos \alpha \\ BD = c-b cos \alpha$

AC = b (по условию)

А значение стороны BC обозначим как a.  
BC = a  
(Именно его нам и нужно найти)

Получим:

$BC^2 - BD^2 = AC^2 - AD^2$

Заменим буквенные обозначения сторон на результаты наших вычислений 

$a^2 - ( c-b cos \alpha )^2 = b^2 - ( b cos \alpha )^2$

перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения - на правую 

$a^2 = ( c-b cos \alpha )^2 + b^2 - ( b cos \alpha )^2$

раскроем скобки

$a^2 = b^2 + c ^2 - 2cb cos \alpha + ( b cos \alpha )^2 - ( b cos \alpha )^2$

получаем 

$a^2 = b^2 + c ^2 - 2bc cos \alpha$

Теорема косинусов доказана.

Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.