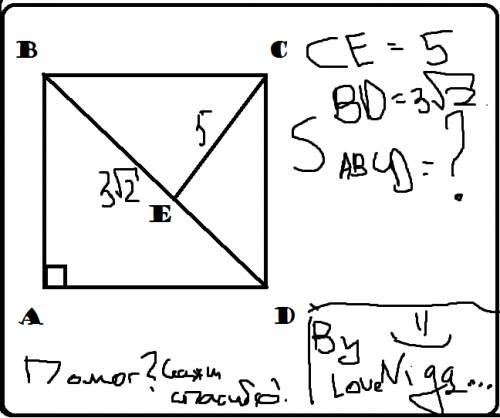
Из точки Е на ВС надо провести перпендикуляр. Пусть он пересекается с ВС в точке К. Тогда ВКЕ - равнобедренный прямоугольный треугольник, и его катеты ВК = ЕК = 3.
В прямоугольном треугольнике ЕКС катет ЕК = 3, гипотенуза ЕС = 5, то есть это "египетский" треугольник, его второй катет равен КС = 4.
Отсюда сторона квадрата ВС = 3 + 4 = 7, а площадь квадрата 7^2 = 49;
На самом деле, есть еще интересная возможность - если ЕD > BD. То есть точка E лежит на продолжении BD за точку B. В этом случае суть решения не меняется, но сторона квадрата ВС = 1, и площадь тоже 1.
R = a / √ (3)
Звідки сторона трикутника дорівнює
a = R * √3 = 4√3
Площа равнестороннего трикутника визначається за формулою
S = √ (3) a² / 4
тобто в нашому випадку
S = √ (3) * (4√ (3)) ^ 2/4 = √ (3) * 16 * 3/4 = 12√ (3)