Опустим из точки O на диагональ AC перпендикуляр OO'. При этом из теоремы о трех перпендикулярах (перпендикуляр SA к плоскости (ABC), наклонная SO', прямая OO' перпендикулярная AO') следует, что отрезок OO' перпендикулярен наклонной SO'. Тогда искомым углом будет угол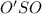 
, обозначим его меру буквой 
.
Из прямоугольного треугольника 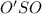(угол 
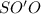равен 90 градусов по-доказанному) найдем 
:
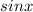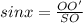-----(1)
В свою очередь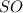 
найдем из прямоугольного треугольника 
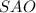( угол 
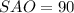градусов, что следует из определения прямой перпендикулярной плоскости) по теореме Пифагора:
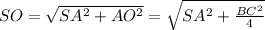------(2)
где по условию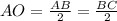 
Из прямоугольного треугольника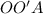 
найдем
длину перпендикуляра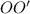 
:
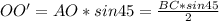--------(3)
И, наконец, подставим в (1) вместо 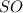и 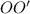выражения (2) и (3), получим:
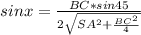
Расчет:
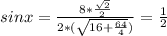
А значит угол 
градусов
1. Поскольку развертка конуса квадрат с диагональю 6, то сторона этого квадрата в √2 раз меньше его диагонали. а=6/√2=6√2/2= см,
площадь боковой поверхности - площадь квадрара S=а²=(3√2)²=9·2=18 (см²)
V=πR²H, где R - радиус основания ,H - высота конуса, равная стороне квадрата.
Найдем R, l=2πR ⇒ R=l/2π = 3√2 /2π (l - длина окружности основания = стороне квадрата)
V=π(3√2/2π)²·3√2=27√2/(2π) ( см³)
2.
Sбок.= 4дм², Sпол. = 6дм², тогда площадь основания Sосн.= 6-4=2дм²
Sосн.=πR² ⇒ R²=Sосн/π=2/π, R=√(2/π),
Sбок.=πRL, гдеL- образующая, ⇒ L = Sбок./(πR)=4/(π√(2/π))=2√2/√π
Зная образующую и радиус основания, найдем высоту конуса:
Н²=L²-R²=(2√2/√π)²-(√(2/π))²=6/π, Н=√6/√π
V=⅓πR²H = ⅓·π·(√(2/π))²·√6/√π=2√6/3√π.
Решаем систему уравнений:
2а+2в = 156
а*в = 720
Из 1 уравнения а = (156-2в)/2 = 78-в.
Подставим во второе:
(78-в)*в = 720
-в²+78в-720 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=78^2-4*(-1)*(-720)=6084-4*(-1)*(-720)=6084-(-4)*(-720)=6084-(-4*(-720))=6084-(-(-4*720))=6084-(-(-2880))=6084-2880=3204;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√3204-78)/(2*(-1))=(√3204-78)/(-2)=-(√3204-78)/2=-(√3204/2-78/2)=-(√3204/2-39)=-√3204/2+39≈10.6980566038302 см;
x_2=(-√3204-78)/(2*(-1))=(-√3204-78)/(-2)=-(-√3204-78)/2=-(-2root3204/2-78/2)=-(-√3204/2-39)=2root3204/2+39≈67.3019433961698 см.
Д = √(а²+в²) = √(10.6980566038302²+67.301943396169²) =
= √(114.45 +4529.6) = √4644= 68.147 см
Длина окружности L = πD = 3.14159*68.147 = 214.0898 см.