ответ: 60 градусов.
Объяснение: Для нахождения угла, образованного высотой и основанием равнобедренного треугольника разделим длину высоты на длину боковой стороны и получим косинус угла: 53/106=0,5. Косинус 0,5 соответствует углу 30 градусов. В равнобедренном треугольнике высота, биссектриса и медиана, проведенные из вершины угла совпадают. Значит угол при вершине будет 30х2=60 градусов. Сумма двух других углов при основании равна 180-60=120 градусов. Величина одного угла будет равна 120/2=60 градусов. В этом треугольнике все углы по 60 градусов
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
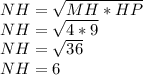
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
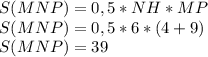
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
Обозначим коэффициент отношения катета ВС и гипотенузы АВ как х.
Тогда АВ=6х,
ВС=5х.
ВА=144
х=144:6=24
ВС=24*5=120
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
ВС²=ВН*АВ
ВН=120²:144
ВН=100
Смотри вложение.