1) 2х + 2(х + 15) = 360
4х + 30 = 360
4х = 330
х = 82 гр 30 мин - 1-ый угол
Тогда 2-ой угол - 82 гр 30 мин + 15 = 97 гр 30 мин.
2) 2х + 2(х - 7,5) = 360
4х - 15 = 360
4х = 375
х = 93 гр 45 мин 1 угол.
Тогда 2 угол - 93 гр 45 мин - 7 гр 30 мин = 86 гр 15 мин.
3) 2х + 2(2х) = 360
6х = 360
х= 60 гр 1 угол
тогда 2 угол - 60 * 2 = 120 гр.
Объяснение:
Найдем угол А: 90 - 27 = 63 градуса(сумма острых углов в прямоугольном треугольнике равна 90 градусов).
Найдем гипотенузу AB.
Синус угла A равен отношению противолежащего данному углу катета BC к гипотенузе AB.
Иначе говоря:
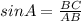
Синус 63 градусов равен 0,891007.
Выразим из этой формулы AB:
AB = BC/sinA = 13/0,891007 = 14,6
Для того, чтобы найти катет AC, мы должны использовать тангенс, т.к. именно эта тригонометрическая функция связывает оба катета.

Тангенс - это отношение противолежащего катета к прилежащему.
Тангенс 27 градусов равен 0,21.
Чтобы найти AC, мы тангенс угла B умножим на BC.
AC = tgB * BC = 0,51 * 13 = 6,63
ответ: два решения (одно для остроугольного треугольника, другое для тупоугольного...)
1) Р = 256 (см)
2) Р = 56V21 (см)
Объяснение: треугольник АВС, основание ВС=2а (чтобы не возиться с дробями); АВ=АС=b
P = 2a+2b = 2(a+b)
а=b*cos(B); по т.синусов: b=2R*sin(B)
S = 2a*h/2 = ah; h = b*sin(B)
S = P*r/2 = (a+b)*r
(a+b)*r = ab*sin(B)
b(1+cos(B))*r = b*b*sin(B)*cos(B)
(1+cos(B))*r = 2R*sin^2(B)*cos(B)
r/(2R) = (1-cos(B))*cos(B)
обозначим х=cos(B)
x^2 - x + (6/25) = 0
(5x)^2 - 5*(5x) + 6 = 0
по т.Виета корни (3) и (2)
5х=3 ---> х = 0.6
---> sin(B) = V(1-0.36) = 0.8 или
5х=2 ---> х = 0.4
---> sin(B) = V(1-0.16) = 0.2V21
b = 2*50*0.8 = 80 или
b = 2*50*0.2V21 = 20V21
a = 80*0.6 = 48 или
а = 20V21*0.4 = 8V21
P = 2*(80+48) = 128*2 = 256 или
Р = 2*(20+8)*V21 = 56V21
1) Пусть первый угол х градусов, второй х+15. х+х+15=180, 2х=165, х=82,5, второй 97,5
2) х+х-7=180, 2х=187, х=93,5, второй 86,5
3) х+2х=180, 3х=180, х=60, второй 120 градусов