Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).
Рис.1
Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD < АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ∠ C > ∠ 1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Доказательство следствия проводится методом от противного.
Из следствия 1 следует, что если три угла треугольника равны, то треугольник равносторонний.
Из теоремы 2 получаем
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается следующая теорема.
Теорема 3. Каждая сторона треугольника меньше суммы двух других сторон.
Следствие 4. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства:
АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.
Т.к. М-середина отрезка АВ, то АМ=МВ. Т.к. основания трапеции параллельные , т.е. ВС//AD, то и К-середина отрезка СD, и => CK=KD. Получаем, что МК- средняя линяя трапеции ABCD. МК=(AD+BC)/2=(10+4)/2=7см
Объяснение:
2. МN - средняя линия треугольника которая, как известно, параллельна его основанию. А основание треугольника в данном случае является и стороной прямоугольника. Противоположные стороны которого (как тоже должно быть известно) параллельны. Стало быть, имеем MN || ВC и ВС || AD => MN || AD=4
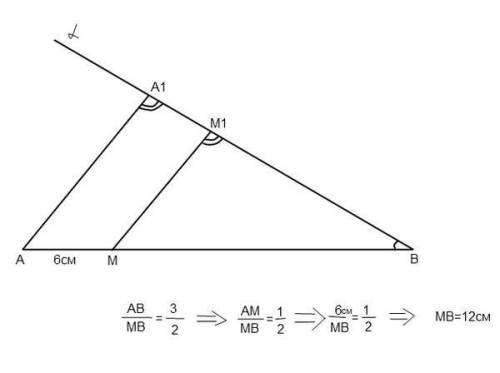
3. А1, М1 и В лежат на одной прямой т. к. эти точки являются точками пересечения с Альфа прямых АВ, АА1, ММ1.
Треугольники АА1В и ММ1В подобны по первому признаку подобия треугольников. (Признак 1 Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника. ) ( угол с вершиной в т. В у них общий, а углы АА1В и ММ1В равны, т. к. АА1 параллельна ММ1)
А так как треугольники подобны то и стороны у них подобны.
Если АА1:ММ1=3:2, то АВ: МВ=3:2 следовательно АМ: МВ=1:2 если АМ=6см, то 6:МВ=1:2 из этой пропорции находим МВ. Получаем МВ=12см
6+7=13
13>12
Треугольник будет тупоугольный.