Задача:
Длина окружности, вписанной в правильный треугольник, равна 12π см. Найдите периметр треугольника.
Чтобы найти периметр правильного Δ, нужно знать сторону; что найти сторону, нужно найти радиус вписанной окружности.
Дня нахождения радиуса окружности, воспользуемся формулой длины окружности и выразим из нее радиус:
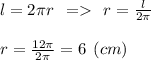
Теперь воспользуемся формулой радиуса вписанной окружности в правильный треугольник для нахождения стороны Δ:
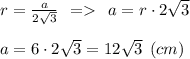
Осталось за малым — периметр правильного треугольника:
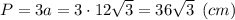
Периметр треугольника равен 36√3 см.
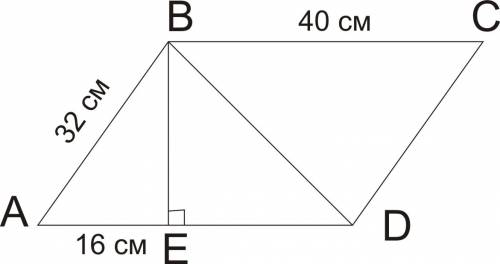
ΔАСК - прямоугольный. В нём АК ==22.По т. Пифагора СА^2 + CK^2 = 484,
CA ^2 =242. CA - 11√2.
А теперь ΔВH D. По т. Пифагора BH^2 + BD^2 = 242. DH^2 =121, BH = 11. Площадь трапеции равна произведению средней линии и её высоты.
S = 11·11 = 121.