Question

Втреугольнике авс угол а 45 с 75 вс=3корня из 2 . найти ас плз

Answer 1

Найдем угол В и затем, чтобы найти сторону АС  воспользуемся теоремой синусов.
угол В=180 градусов-(45 градусов+75 градусов)=60 градусов
Угол В лежит напротив сторона АС, угол А лежит напротив ВС. Получим:
$\frac{sin B}{AC}= \frac{sinA}{BC};AC= \frac{BC*sinB}{sinA}; AC= \frac{3 \sqrt{2}*sin 60^0 }{sin 45^0}= \frac{3 \sqrt{2}* \frac{ \sqrt{3} }{2} }{ \frac{ \sqrt{2} }{2} } =$$\frac{3 \sqrt{2*3}}{2}* \frac{2}{ \sqrt{2} } =3 \sqrt{3}$

Answer 2

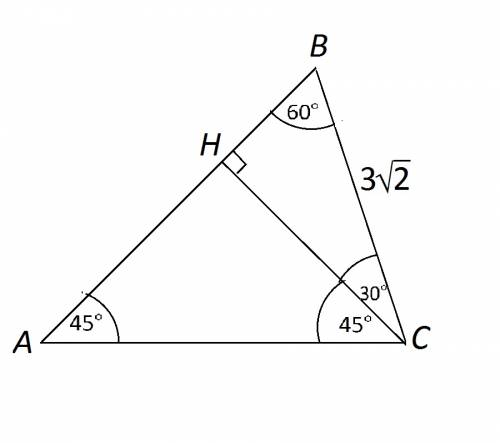
Вариант решения. 

Проведём из С к АВ высоту СН

Она разделила угол С на углы 45° и 30° 

Получены треугольник ВНС с углами 30° и 60°и равнобедренный АНС с 45° при основании АС.

СН из треугольника ВНС равен ВС*sin (60°)=(3√2)*(√3):2.

Умножив числитель и знаменатель в значении СН на √2, получим (3√3):√2

Гипотенуза  равнобедренного прямоугольного треугольника равна а√2

АС=АВ*√2={(3√3):√2}*√2=3√3

--------

Или: 

СН, как противолежащий углу 30° катет, равен половине ВС и равен 1,5√2

Тогда по т. Пифагора СН²=ВС²-ВН²=18-4,5=13,5

АН=СН

АС²=АН²+СН²=13,5+13,5=27

АС=√27=√9*√3=3√3

Как видим, любой вариант дает одинаковый ответ.