Дано тр. ABC
К, M - середины AB и ВС
AB=BC
BD - медиана
Док-ть:
тр. BKD = тр. BMD
Док-во:
так как K и M по условию середины сторон AB и ВС, то KM - средняя линия тр. ABC
AB=BC (по условию тр. равнобедренный), след-но BK=BM и угол BKM = углу BMK (углы при основании равнобедренного тр.)
BD - медиана (из определения - отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны), след-но KD=DM
Значит по первому признаку равенства треугольников: Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
эти треугольники равны (BK=BM, KD=DM, угол BKM = углу BMK)
Подробнее - на -
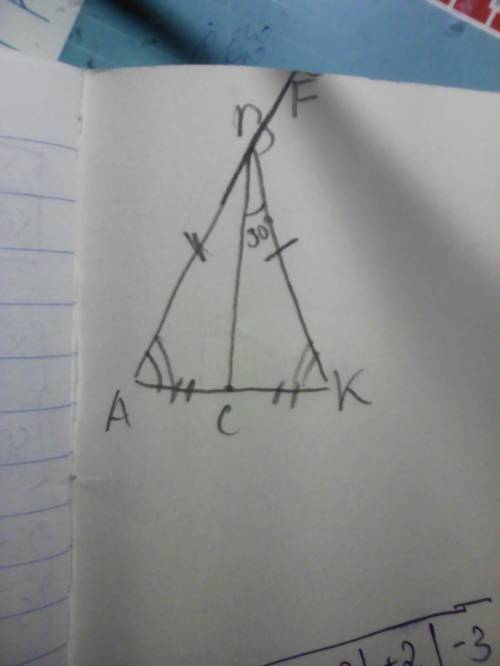
Рассм. ΔАВК
АВ = ВК по условию ⇒ ΔАВК - равнобедренный по определению
∠ А = ∠С по св-ву равнобедренного треугольника
Рассм. ΔАВС и ΔКВС
∠ А = ∠С по св-ву равнобедренного треугольника
АВ = ВК по условию
АС = СК по условию ⇒ ΔАВС = ΔКВС по двум сторонам и углу между ними, значит все их соответственные элементы равны, а в частности:
∠АВС = ∠СВК
∠СВК = 30° по условию ⇒ ∠АВС = 30°
Рассм. ΔАВК
∠АВС = ∠СВК = 30°
∠АВК = ∠АВС + ∠СВК = 30° + 30° = 60°
Сделаем дополнительное построение, продлим отрезок АВ дальше и назовём луч, который выходит из точки В, лучом ВF
∠ FBK и ∠ABK - смежные, по св-ву смежных углов ∠ FBK + ∠ABK = 180°, а ∠ABK = 60° ⇒ ∠ FBK = 180° - 60° = 120°
ответ: ∠ FBK = 120°
y=3x+5;⇒k₁=3;b=5;
x+3y-1=0;⇒y=-1/3x+1/3;k₂=-1/3;b=1/3;
условие перпендикулярности прямых:k₁·k₂=-1;
k₁·k₂=3·(-1/3)=-1;
данные прямые перпендикулярны
3x-4y+7=0;⇒
y=3/4x+7/4;⇒k₁=3/4;
6x-8y+1=0;⇒
y=6/8x+1/8;⇒k₂=6/8=3/4;
k₁=k₂⇒прямые параллельны