Объяснение:
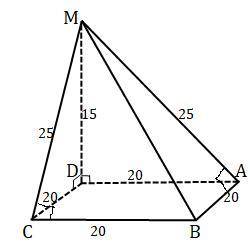
S(бок)= S(МDА)+S(МDС)+S(МАВ)+S(МСВ)
1)Т.к. МD⊥(АВС) , то МD⊥DА , МD⊥DС.
Δ МDА= МDС как прямоугольные по 2-м катетам : МD-общая, АD=DС как стороны квадрата , S(МDА)=S(МDС)=1/2*20*15=150(см²).
2) МD⊥( АВС), DА⊥АВ , значит МА⊥АВ по т. о 3-х перпендикулярах⇒ΔМАВ-прямоугольный.
МD⊥( АВС), DС⊥СВ , значит МС⊥СВ по т. о 3-х перпендикулярах⇒ΔМСВ-прямоугольный.
3) ΔМАВ= ΔМСВ, как прямоугольные по катетам МА=МС=25 и общей гипотенузе МВ. Поэтому S(МАВ)=S(МСВ)=1/2*20*25=250 (см²).
4)S(бок)= 2*150+2*250=800 (см²).
Пусть ∠А=9х, ∠В=2х, ∠С=7х
Тогда
∠А : ∠В : ∠С=9 : 2 : 7
Сумма углов треугольника равна 180°.
∠А + ∠В + ∠С =180 °
9х + 2х + 7х = 180
18х = 180°
х=10°
∠А=9·10°=90° , ∠В=2·10°=20°, ∠С=7·10°=70°
ответ.Треугольник АВС - прямоугольный.
2.
Пусть в треугольнике второй угол равен х°, первый угол равен (х+64)ᵒ, а третий равен 2х°.
Сумма углов треугольника равна 180°.
х+(х+64)+2х=180
4х+64=180
4х=180-64
4х=116
х=29°
ответ. Второй угол равен 29°, первый угол равен (29+64)ᵒ=93°, а третий равен 58°.