
ответ: угол В=80
Объяснение: рассмотрим ∆АОС. Он тоже является равнобедренным, поскольку биссектрисы проведены из равных углов. Теперь вычислим углы ОАС и ОСА. Биссектрисы углов А и С
делят их пополам. Сумма углов в треугольнике равна 180° и поэтому:
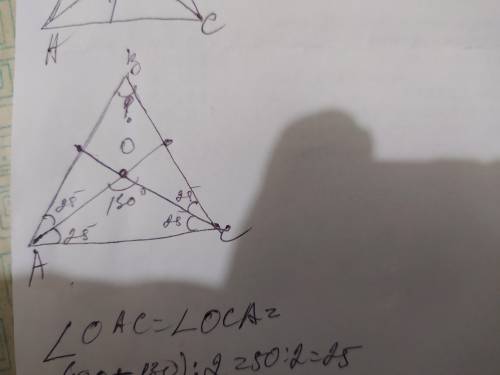
180- 130=50. Сумма этих углов=50. Так как они равны: 50÷2=25. Угол ОАС= углу ОСА=25°. Так как угол А и С разделяют биссектрисы, то угол ВАО равен углу ВСО и тоже равны 25°. Следовательно угол А= углу С=50°. Теперь найдём угол В. Угол В = 180-50-50=80
дано: ab=ad,
∠bac=∠dac
доказать: ∆abc=∆adc
доказательство:
1) ab=ad (по условию)
2) ∠bac=∠dac (по условию)
3) ac — общая сторона.
следовательно, ∆abc=∆adc (по двум сторонам и углу между ними)
дано:
ao=bo,
co=do
доказать: ∆aoc=∆bod.
доказательство:
определяем те элементы, о равенстве которых известно по условию :
1) ao=bo (по условию)
2) co=do (по условию).
3) ∠aoc = ∠bod (как вертикальные).
дано:
ab=ac,
af=ak
доказать: ∆abk=∆acf
доказательство:
1) ab=ac (по условию)
2) af=ak (по условию)
3) ∠a — общий.
следовательно, ∆abk=∆acf (по двум сторонам и углу между ними).
вычислите периметр равнобедренного треугольника авс, если периметр треугольника adc равен 18 cм, и cd = 6 cм и ad = bd (fig.5)
доказательство:
периметр треугольника adc = ac + cd + ad = 18 ⇔ ac + 6 + ad = 18 ⇔ ac + ad = 12
потому что ac = bc (треугольники являются равнобедренными) и ad = db, следовательно ac + ad = db +bc = 12
периметр треугольника abc = ab + ac + bc = ad + db + ac + bc = 12 + 12 = 24 cм.