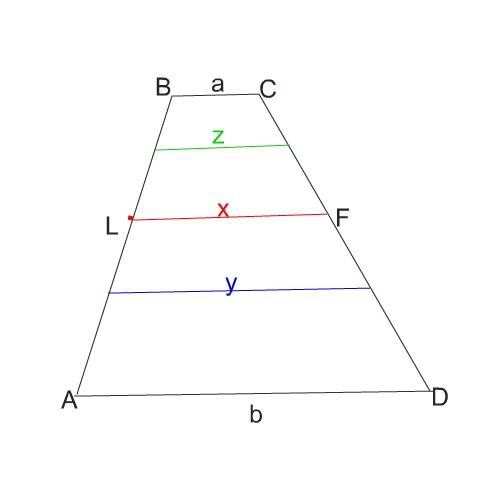
Обязательно смотрим рисунок.
И примем во внимание, что получающиеся трапеции подобны не исходной.
Если трапеции ALFD и LBCF подобны, то a/LF = LF/b.
Отсюда LF = √(ab).
Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.
---
Делим трапецию:
1 отрезок между основаниями исходной:
х²=2*8=16
х=√16=4
Второй отрезок между первым и основанием исходной трапеции
у²=4*8=32
у =√32=4√2
Третий отрезок - идет под меньшим основанием
z²=2*4=8
z=2√2
---------------------------
Отрезки в рисунке идут в таком порядке
z, x, y
---------------
Коэффициент подобия между этими четырьмя трапециями попарно ( смежными) равен
4:2√2=2:√2=2√2:√2·√2=2√2:2=√2
k=√2
Площади подобных фигур относяся как квадрат коэффициента их подобия.
Для этих трапеций это
(√2)²=2
Площадь второй по величине относится к нижней -большей- как 1:2=1/2
Третьей ко второй 1/2:2=1/4
и последней
1/8
сложим площади
1/2+1/4+1/8 =( 4+2+1)/8=7/8
7/8 < 1
Площадь самой большой из этих четырёх трапеций больше суммы площадей остальных трёх
Объяснение:
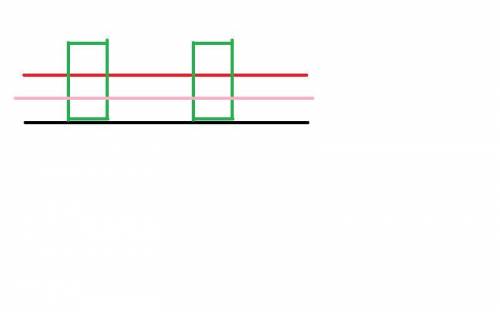
Задачи обе на логику, учтём что линейка имеет форму прямоугольника(следов все углы 90градусов) .
1. прикладываешь линейку как на рисунке в двух местах( получается прямой угол) , отмеряешь одинаковое расстояние , ставишь две точки и проводишь линию, она будет перпендикулярна, т.к. линия, содержащая две точки , равноудалённые от другой линии , паралельна данной(соответственно им двум)
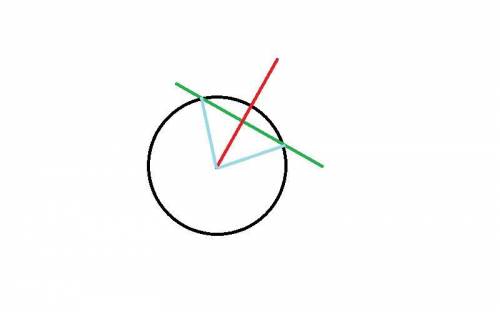
2.берём линейку проводим хорду, меряем расстояние между прямой А и Б , делим его на 2(находим центр) ,проводим через него линию , это и будет перпендикуляр , в качестве доказательства проведём к точкам А и Б линии , равные (они будут равны радиусу окружности) , следовательно полученный треугольник будет равнобедренным, а в равнобедренном треугольники перпендикуляр находится как раз в центре
угол CDE = 180-120=60°
угол DCE = 180-90-60=30°
Катет лежащий напротив угла 30° равен половине гипотенузы
CE=2×DE=2×7=14 (см)