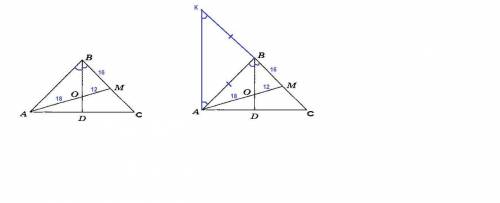
ВD - высота равнобедренного треугольника, проведенная к основанию, значит и биссектриса.
Биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.
В треугольнике АВМ ВО - биссектриса, значит
АО : ОМ = ВА : ВМ
ВА = АО · ВМ / ОМ = 18 · 16 / 12 = 24 см
Доказательство свойства биссектрисы (на всякий случай)
Проведем прямую АК║BD, К - точка пересечения этой прямой с прямой ВС.
∠DBA = ∠KAB как накрест лежащие (AK ║ BD, AB секущая),
∠CBD = ∠СКА как соответственные (АК ║ BD, СК секущая),
так как ∠DBA = ∠CBD, то и ∠КАВ = ∠СКА, тогда
ΔАВК равнобедренный, АВ = ВК.
По обобщенной теореме Фалеса:
АО : ОМ = КВ : ВМ или
АО : ОМ = АВ : ВМ.
S = 8·π/(1 - Cos40) см².
Объяснение:
Из формулы суммы углов правильного многоугольника:
180°(n-2) = 1260 => n = 9. Сторона многоугольника равна 36/9 = 4 см.
Правильный девятиугольник, вписанный в окружность радиуса R делится на 9 равных равнобедренных треугольников с боковыми сторонами, равными R и основанием, равным 4 см. Угол при вершине такого треугольника равен 360°/9 = 40°. Тогда по теореме косинусов имеем: 4² = R²+R²- 2·R·R·Cos40. => 16 = 2R²(1 - Cos40) =>
R² = 8/(1 - Cos40) см².
Площадь круга равна S = πR² = 8·π/(1 - Cos40).