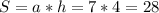кв. ед.
Запишем векторы c и d через проекции
с(4; 2) d(5; -2)
Модули векторов
|c| = √(4² + 2²) = √20 |d| = √(5² + (-2)²) = √29
a) Скалярное произведение
c · d = (4 · 5 + 2 · (-2) =20 - 4 = 16
Найдём угол α между векторами
c · d =|c| · |d| · cosα
cos α = (c · d) : (|c| · |d|) = 16 : √(20 · 29) ≈ 0.664
α ≈ 48°
б) Найдём сумму векторов
e = c + d e(4+5; 2-2) e(9; 0)
|e| = 9
в) Найдём разность векторов
f = c- d f(4-5; 2-(-2)) f(-1; 4)
|f| = √((-1)² + 4²) = √17 ≈ 4.12
г) Найдём вектор g = -2c + 0.5d
g(-2·4+0.5·5; -2·2+0.5·(-2))
g(-5.5; -5)
Модуль вектора g
|g| = √((-5.5)² +(-5)²) ≈ 7.43
Основания трапеции равны 5 см и 45 см, площадь трапеции равна 375 см².
Объяснение:
Высоты трапеции BF и CE равны диаметру вписанной окружности.
Прямоугольные треугольники ABF и DCE равны.
По теореме Пифагора на ходим сторону ЕD треугольника ECD:
ED²=CD²−CE²;
ED²=252−152;
ED=(252−152
ED=20 см.
Суммы противоположных сторон трапеции равны, так как в трапецию вписана окружность.
BC + AD = AB + CD;
BC = FE,
Пусть BC = x,
Тогда x+20+x+20=25+25;
x=5.
Получается:
BC= 5 см, AD= 20+5+20 = 45 см.
Площадь трапеции S = BC + AD2 * EC = 5 + 452*15 = 375 см².
