
В таких заданиях в основном ведётся работа с формулами. Прежде, чем притупить к заданям, вспомним формулу основного тригоносетрического тождества, которая в основном тут и будет использоваться:
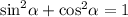
1) Если мы воспользуемся основным тригоносетрическим тождеством, выразив оттуда косинус в квадрате, то получим как раз таки это выражение, значит его можно упростить так:
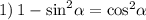
2) Аналогично предыдущему, тоже опираясь на основное тригоносетрическое тождество, получим:
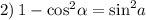
3) Это выражение для начала можно сложить по формуле разности квадратов, после чего преобразуем полученное выражение так же, как и во втором:
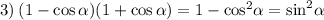
4) Опять же, опираясь на основное тригоносетрическое тождество можно синус в квадрате плюс косинус в квадрате заменить на единицу, в результате чего мы получим:
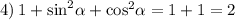
5) Вынесем за скобку синус, а полученное выражение преубразуем, опять же, как во втором пункте:
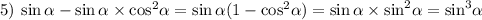
АС и B1D1 - это скрещивающиеся диагонали противоположных граней (оснований), поэтому расстояние между ними равно высоте призмы (или боковым ребрам).
ВВ1 = 5;
Что касатеся основного вопроса задачи, то ответ лежит на поверхности. Нужно найти угол (косинус) между плоскостями, перпендикулярными ВD1 и ВВ1 (это - плоскость основания :)). Поскольку эти прямые пересекаются в точке В, нужный угол очевидно равен углу D1BB1 - как бы не была расположена плоскость сечения и как бы не был построен искомый линейный угол двугранного угла, его стороны будут перпендикулярны сторонам угла D1BB1 .
Осталось найти диагональ BD1
BD1^2 = 12^2 + 31 + 5^2 = 200; BD1 = 10√2;
cos(угол D1BB1) = В1В/D1B = 5/(10√2) = √2/4;