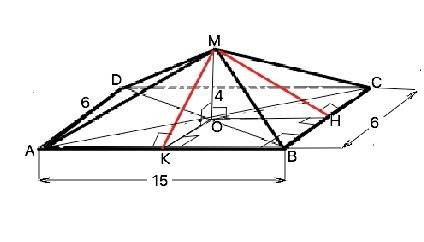
Пусть в пирамиде МАВСD стороны AD=BC=6 см, AB=CD=15 см. По условию высота МО=4 см, О - точка пересечения диагоналей основания. Площадь боковой поверхности пирамиды равна сумме площадей боковых граней. Так как диагонали прямоугольника равны и точкой пересечения делятся пополам, боковые грани - две пары равных равнобедренных треугольников. Ѕ(бок)=2•Ѕ(ВМС):2+2•Ѕ(АМВ):2=Ѕ(ВМС)+Ѕ(АМВ) Высоты МК и МН боковых граней перпендикулярны сторонам основания, их проекции по т. о 3-х перпендикулярах также перпендикулярны сторонам основания, параллельны соседним сторонам и равны их половине. ОК=СВ:2=3 см, ОН=АВ:2=7,5 см. Высоты боковых граней - гипотенузы прямоугольных треугольников МОК и МОН и по т.Пифагора МК= 5 см, МН=8,5 см. Ѕ(бок)=5•15+8,5•6=126 см²
= 2/v5; ctg= cos/sin =v5/3:2/3=v5/2.
2) sin=1/4; cos =v15/4; tg=1/v15;ctg=v15.