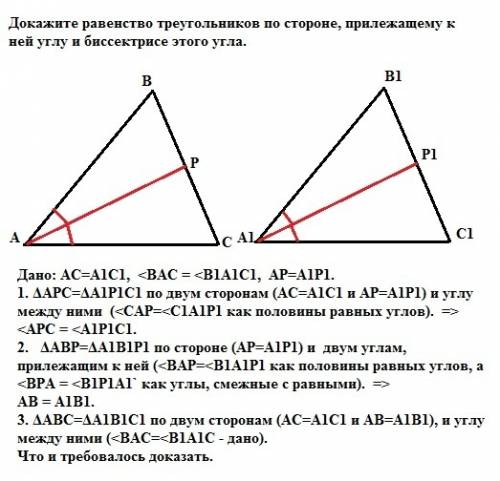
Дано: АС=А1С1, <BAC = <B1A1C1, АР=А1Р1.
1. ΔАРС=ΔА1Р1С1 по двум сторонам (АС=А1С1 и АР=А1Р1) и углу между ними (<CAP=<C1A1P1 как половины равных углов). => <APC=<A1P1C1.
2. ΔАВР=ΔА1В1Р1 по стороне (АР=А1Р1) и двум углам, прилежащим к ней (<ВAP=<В1A1P1 как половины равных углов, а <BPA = <B1P1A1` как углы, смежные с равными). => AB = A1B1.
3. ΔАВС=ΔА1В1С1 по двум сторонам (АС=А1С1 и АВ=А1В1), и углу между ними (<ВАС=<В1A1С - дано).
Что и требовалось доказать.