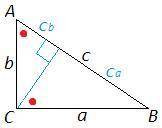
в) c_a= a *sinA = 8*√3/2 =4√3
b= a *ctgA = 8*√3/3
c_b= b *cosA = 8*√3/3 *1/2 =4√3/3
г) a= c *sinA =6*1/2 =3
c_a= a *sinA =3*1/2 =3/2
b= c *cosA =6*√3/2 =3√3
c_b = b *cosA =3√3 *√3/2 =9/2
Или
Высота из прямого угла делит гипотенузу отрезки, которые относятся как квадраты прилежащих катетов. В треугольнике с углами 30, 60, 90 стороны относятся как 1:√3:2.
в) a=8: b=8/√3, c=16/√3
c_a/c_b =(a/b)^2 =3/1
c_a =16/√3 *3/4 =4√3
c_b =16/√3 *1/4 =4√3/3
г) с=6: a=3, b=3√3
c_a/c_b =(a/b)^2 =1/3
c_a =6 *1/4 =3/2
c_b =6 *3/4 =9/2
Объяснение:
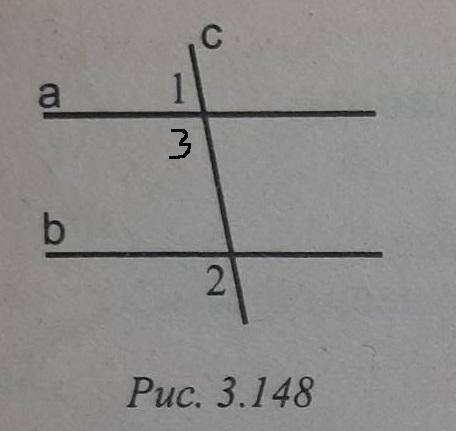
Во вложении рисунки к 1 и 3 задачам.
1) <1 и <3 - смежные, а <2 и <3 - соответственные, значит <2=<3, а <1+<3=<1+<2=180.
х -1 часть. 4х+5х=180; 9x=180; x=20;
<1=4x=4*20=80°; <2=5x=5*20=100°.
2) Из равенства <1=<2 следует, что a ll b при секущей AB как соответственные. => <3+<4=180 как односторонние при секущей BC. При этом <3=<4+30. =>
<4+30+<4=180
2*<4=150
<4=75°
<3=75+30=105°
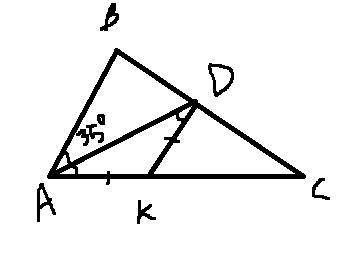
3) Так как AD - биссектриса, то <BAD=<KAD=35°.
DK=AK по условию, значит △ADK - равнобедренный. => <KAD=<KDA=35°.
Сумма углов тр-ка равна 180°, значит <AKD=180-2*35=110°
№1
№1Дано:
ABCD – параллелограмм,
DE – высота, равная 4,
CD=8.
Найти: S(ABCD)
Найти: S(ABCD)Решение:
S=a*h, где S – площадь параллелограмма, а – сторона параллелограмма, h – высота параллелограмма, проведенная к этой стороне.
Противоположные стороны параллелограмма равны, следовательно AB=CD=8.
S=AB*DE=8*4=32.
ответ: 32.
№2
Дано:
ABCD – параллелограмм,
BD – высота и диагональ параллелограмма, равная 13,
AD=12
Найти: S(ABCD)
S=a*h, где S – площадь параллелограмма, а – сторона параллелограмма, h – высота параллелограмма, проведенная к этой стороне.
S=AD*BD=12*13=156.
ответ: 156.
№3
Дано:
ABCD – параллелограмм,
ВН – высота, равная 5,
AH=12,
AB=13,
HD=3.
Найти: S(ABCD)
S=a*h, где S – площадь параллелограмма, а – сторона параллелограмма, h – высота параллелограмма, проведенная к этой стороне.
S=AD*BH=(AH+HD)*BH=(12+3)*5=15*5=75.
ответ: 75.
= решение = решение = решение = решение = решение =