.(Сторона ромба с его диагоналями образует углы, разность которых равна 15 градусов. найдите углы ромба.).

👇

Увидеть ответ

Ответ:

dubonosova37

10.10.2021

угол ромба в два раза больше угла стороны ромба и его диагонали

следует разность между углами будет в два раза больше 15*2=30

сумма двух углов ромба, принадлежащих одной стороне =180* (*-градусы)

значит (180-30)/2=75 -одна пара углов ромба = кажый из углов

75+30=105* - каждый из углов второй пары

4,7(7 оценок)

Открыть все ответы

Ответ:

глупыйоладушек

10.10.2021

Дано: ABC - равнобедренный треугольник; AB = BC = 13дм, АС = 10см.
Найти: $a)\,\,BK;\,\, b)\,\, S_{ABC};\,\,c)\sin A,\,\cos A,\, tg\, A,\,ctg \,A$
решение:
У равнобедренного треугольника боковые стороны и углы при основания равны
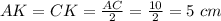
С вершины В проведём перпендикулярно к стороне основанию АС высоту ВК. Делит она сторону на отрезки: $AK = CK = \frac{AC}{2} = \frac{10}{2} =5\,\, cm$
С прямоугольного треугольника ABK ( ∠AKB=90°):
По т. Пифагора высота ВК равна:
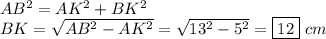
$AB^2=AK^2+BK^2 \\ BK= \sqrt{AB^2-AK^2} = \sqrt{13^2-5^2}=\boxed{12}\,\,cm$
Площадь равнобедренного треугольника равна произведению стороны основания на высоту делённое на 2
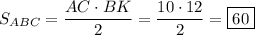
$S_{ABC}= \dfrac{AC\cdot BK}{2} = \dfrac{10\cdot 12}{2} =\boxed{60}$
Синус угла - это отношение противолежащего катета к гипотенузе:
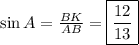
$\sin A= \frac{BK}{AB} = \boxed{\frac{12}{13}}$
Косинус угла - это отношение прилежащего катета к гипотенузе:
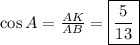
$\cos A= \frac{AK}{AB} = \boxed{\frac{5}{13}}$
Тангенс угла - это отношение противолежащего катета к прилежащему катету
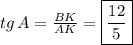
$tg \, A= \frac{BK}{AK} = \boxed{\frac{12}{5}}$
Котангенс угла - это отношение прилежащего катета к противолежащему катету
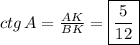
$ctg \, A= \frac{AK}{BK} = \boxed{\frac{5}{12}}$

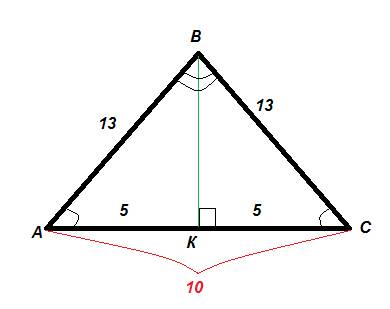
Вравнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. найдите: а)высоту

Вравнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. найдите: а)высоту

4,4(98 оценок)

Ответ:

260г

10.10.2021

Теорема d3. В равнобедренном треугольнике высоты, опущенные к боковым сторонам, равны.

Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его высоты. Тогда углы ABL и KAB равны, так как углы ALB и AKB прямые, а углы LAB и ABK равны как углы при основании равнобедренного треугольника. Следовательно, треугольники ALB и AKB равны по второму признаку равенства треугольников: у них общая сторона AB, углы KAB и LBA равны по вышесказанному, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Если треугольники равны, их стороны AK и BL тоже равны. Что и требовалось доказать

Объяснение:

4,7(37 оценок)

Это интересно:

Транспорт

26.01.2020

Как смазать велосипедную втулку: простые советы от эксперта...

Искусство-и-развлечения

20.02.2022

Как узнать своих персонажей: советы для писателей...

Здоровье

13.09.2021

Как избавиться от большого волдыря за короткий промежуток времени...