Sc = d²·tgα·√2/(2+tgα).
Sб = 4d²·tgα/(2+tgα).
So = d²/(2+tgα).
So =
Объяснение:
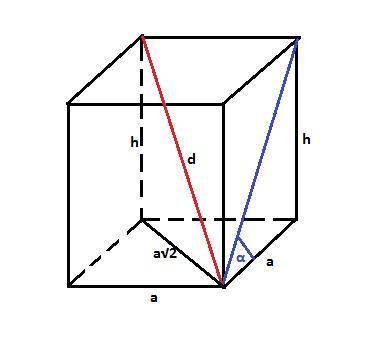
Призма правильная, значит в основании лежит квадрат. Пусть сторона квадрата равна "а". Тогда диагональ квадрата равна а√2.
Высота призмы равна h = a·tgα (из прямоугольного треугольника - половины боковой грани).
Квадрат диагонали призмы d² = h²+2a². (из прямоугольного треугольника - половины диагонального сечения).
d² = a²·tg²α+2a² = a²(2+tgα). => a = d/(√((2+tgα)).
h = a·tgα = d·tgα/(√((2+tgα)).
Тогда площадь диагонального сечения равна:
Sc = a√2·h = d√2/(√(2+tgα))·dtgα/(√(2+tgα)) = d²·tgα·√2/(2+tgα).
Площадь боковой поверхности равна произведению периметра основания на высоту призмы:
Sб = 4·a·h = 4d/(√((2+tgα))·d·tgα/(√((2+tgα)) = 4d²·tgα/(2+tgα).
Площадь основания (квадрата) равна квадрату стороны:
So = a² = d²/(2+tgα).
S полная = 2 * Sоснований + 4 * Sбоковые
2 * Sоснований, т.к. верхнее основание и нижнее основание, а они равны.
4 * Sбоковые, т.4 у правильной четырехугольной призмы 4 боковые поверхности и они тоже равны.
2* Sоснований = 40 - 32 = 8 кв. см.
Sоснования= 4 кв.см, в основании лежит квадрат значит его сторона а = 2 см
4 * Sбоковые = 32
Sбоковая = 8
Sбоковая = а * h, отсюда h = Sбок : а = 8 : 2 = 4
ответ. h = 4 см