
В правильной усеченной четырехугольной пирамиде диагонали оснований равны 10 см и 6 см, а боковая грань образует с плоскостью основания угол 60 градусов. Найти высоту усеченной пирамиды.
Объяснение:
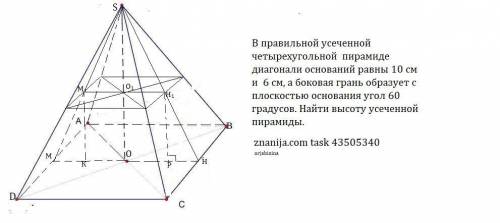
1) АВСDA₁B₁C₁D₁- усеченная пирамида , Точки О и О₁ -точки пересечения диагоналей оснований Т.к пирамида правильная , то основания кавдраты.
АВСD- нижнее основание , по т. Пифагора АВ=√(10²:2)=5√2 (см).
A₁B₁C₁D₁-верхнее основание , по т. Пифагора A₁B₁=√(6²:2)=3√2 (см).
2) Проведем через точки О и О₁ отрезки МН и М₁Н₁ перпендикулярно сторонам квадратов.Тк О₁Н₁ ⊥ВС, то SH⊥ВС по т. о трех перпендикулярах . Поэтому линейным углом между плоскостью боковой грани и плоскостью основания будет ∠НН₁М=60°.
3) Рассмотрим сечение , проходящее через МН и М₁Н₁ перпендикулярно сторонам основаниям. В сечении получилась равнобедренная трапеция ММ₁Н₁Н.
Проведем высоты М₁К и Н₁Р в трапеции . Тогда КР=М₁Н₁ =3√2 см , а МК=РН=( 5√2-3√2):2=√2 (см).
ΔРНН₁ -прямоугольный , tg60°=PН₁ /PH , √3=PН₁ /√2 , PН₁ =√6 см.
Поэтому высота усеченной пирамиды √6 см.
Латиница заменена русскими
Трапеция АВСД, проводим биссектрису угла В до пересечения с со стороной АД - точка Р, угол АРВ=углуРВС как внутренние разносторонние = углу АВР, треугольник АВР равнобедренный АВ=АР=13, АФ - биссектриса угла А = медиане, высоте , точка Ф середина ВР, проводим линию ФК параллельно АР до пересечения с АВ , ФК стредняя линия треугольника АВЗ = АР/2=13/2=6,5,
продлеваем биссектрису углаС до пресечения со стороной АД - точка Т, угол СТД=углуТСВ как внутренние разносторонние =углуТСД, треугольник ТСД равнобедренный, ТД=СД=15,
ДГ биссектриса угла Д = медиане, высоте, точка Г лежит на середине ТС, проводим ГМ параллельноТД до пересечения с СД, ГМ=средняя линия треугольника ТСД = 1/2ТД =15/2=7,5, Линия КМ-средняя линия трапеции = 1/2(ВС+АД)=1/2(16+30) =23
ФГ= КМ-КФ-ГМ=23-6,5-7,5=9