10 см.
Объяснение:
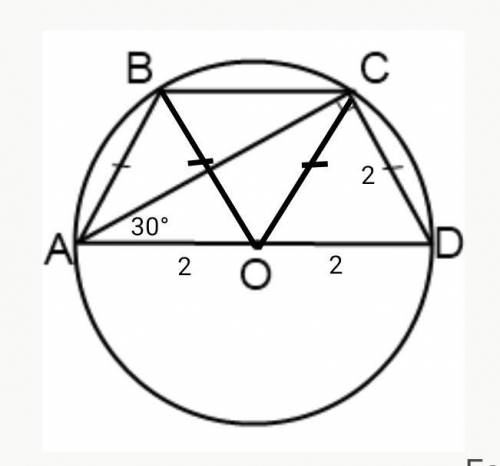
1. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. С другой стороны, сумма углов, прилежащих к боковой стороне трапеции, тоже равна 180°, тогда углы при основаниях трапеции равные, и отсюда следует, что вписать в окружность можно только равнобедренную трапецию. В нашем случае трапеция АВСD равнобедренная, АВ = СD = 2 см, ∠CAD = 30°.
2. Так как по условию центр описанной окружности лежит на большем основании, то ∠ АСD вписанный, опирающийся на диаметр, тогда по теореме ∠ АСD = 90°.
3. В прямоугольном треугольнике ACD напротив угла в 30° лежит катет, равный половине гипотенузы, тогда AD = 2•CD = 2•2 = 4 (см).
4. ∆ABO и ∆DCO равные равносторонние, все их углы по 60°, тогда и в равнобедренном ∆BOC ∠BOC = 180° - (60°+60°) = 60°, тогда и он равносторонний, ВС = ОВ = ОС = 2 см
5. Р ABCD = 4 + 2 + 2 + 2 = 10 (см)
10 см.
Объяснение:
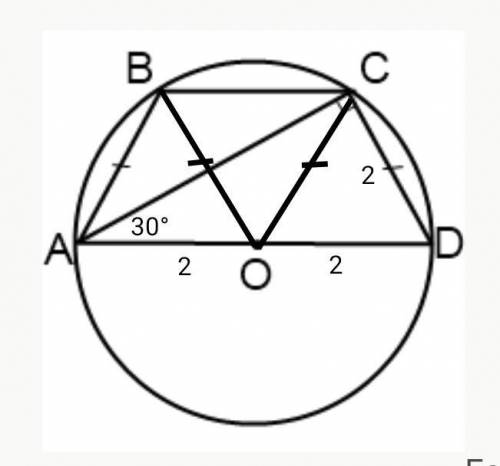
1. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. С другой стороны, сумма углов, прилежащих к боковой стороне трапеции, тоже равна 180°, тогда углы при основаниях трапеции равные, и отсюда следует, что вписать в окружность можно только равнобедренную трапецию. В нашем случае трапеция АВСD равнобедренная, АВ = СD = 2 см, ∠CAD = 30°.
2. Так как по условию центр описанной окружности лежит на большем основании, то ∠ АСD вписанный, опирающийся на диаметр, тогда по теореме ∠ АСD = 90°.
3. В прямоугольном треугольнике ACD напротив угла в 30° лежит катет, равный половине гипотенузы, тогда AD = 2•CD = 2•2 = 4 (см).
4. ∆ABO и ∆DCO равные равносторонние, всё их углы по 60°, тогда и в равнобедренном ∆BOC ∠BOC = 180° - (60°+60°) = 60°, тогда и он равносторонний, ВС = ОВ = ОС = 2 см
5. Р ABCD = 4 + 2 + 2 + 2 = 10 (см)
Углы ВАС и CAD по 30°, значит угол CDA = 180 - 90 - 30 = 60°, поэтому трапеция равнобедренная и AB = CD.
Треугольник АВС - равнобедренный (2 угла по 30°), поэтому ВС = АВ.
Катет, противолежащий углу 30°, вдвое меньше гипотенузы, поэтому
AD = 2 * AB.
Если принять АВ = х, то AD = 2 * x. Получаем уравнение
х + х + х + 2 * х = 5 * х = 20 , откуда х = 4.
Следовательно AD = 2 * 4 = 8 см.