
ответ: AB и CD – 8 (ед. длины); BC и AD – 12 (ед. длины)
Объяснение:
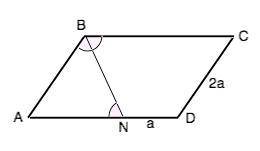
ND=CD/2 Примем ND=a. Тогда CD=2a, AB=CD=2a.
ВС||AD, BN – секущая => ∠СВN=∠BNA – накрестлежащие при пересечении параллельных прямых секущей. Но ∠СВN=∠АВN как половина угла АВС ( BN – биссектриса) =>
∠ANB=∠АВN.
В треугольнике АВN углы при основании BN равны. ∆ АВN- равнобедренный. => AN=AB=2a =>
AD=AN+ND=2a+a=3a. BC=AD=3a
P(ABCD)=AB+CD+BC+AD=2•(2a+3a)=10a
10a=40
a=4
AB=CD=2•4=8 (ед. длины)
BC=AD=3•4=12 (ед. длины)
Площадь S1 боковой поверхности призмы равна произведению периметра перпендикулярного сечения призмы на её боковое ребро. Плоскость перпендикулярного сечения пересекает боковые грани по их высотам. Поэтому периметр перпендикулярного сечения равен сумме этих высот, т. е. 3*2=6.
Значит, S1 = 3al = 18
ПустьS -- площадь основания призмы. Площадь ортогональной проекции основания призмы на плоскость, перпендикулярную боковым рёбрам, равна площади перпендикулярного сечения, делённой на косинус угла между плоскостями основания и перпендикулярного сечения. Этот угол равен углу между боковым ребром и высотой призмы, т. е. 60∘.
Поэтому
S2= 2√3Следовательно, площадь полной поверхности призмы равна