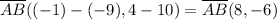 ;
; от точки A
от точки A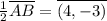 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: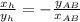 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 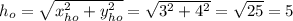 ;
;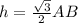 , т.к
, т.к 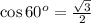 ;
;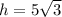 , а стало быть
, а стало быть  ;
;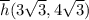 .
.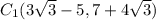 /// примечание:
/// примечание: 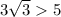 ;
;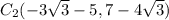 /// примечание:
/// примечание: 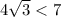 .
.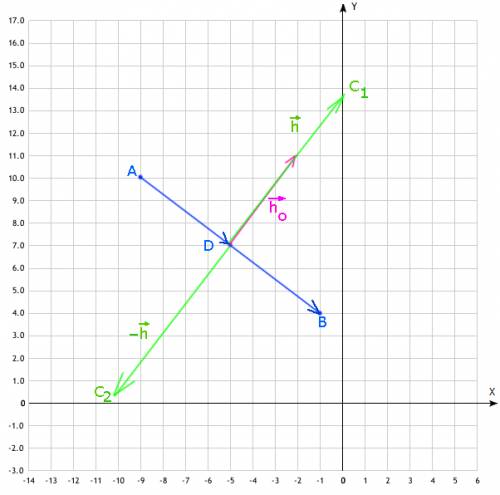
У нас получается параллелограмм АВСЕ, ВЕ и АС - диагональ. По свойству в параллелограме противолежащие стороны и углы равны => ВС = АЕ, ВА = СЕ. В параллелограме ВСDЕ по тому же свойству ВС = ЕD, ВЕ = СD. ВС = АЕ = ЕD, а значит равен 1/2 отрезка AD. Ч.т.д.