Примем коэффициент отношения данных углов равным а.
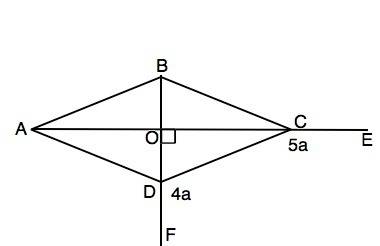
Тогда ∠FDC=4a; ∠ECD=5a
Угол ОDF развернутый, ⇒ угол ODC=180°-4a
Угол ОСЕ - развернутый ⇒ угол ОСD=180°-5а.
Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам.
∆ DOC прямоугольный.
Сумма острых углов прямоугольного треугольника =90°.
180°-4а+180°-5а=90°
9а=270° ⇒
а=30°
Угол ВDC=180°-4•30°=60°
Противолежащие углы ромба равны.
Угол АВС=АDC=2•∠BDC=120°
Сумма углов. прилежащих к одной стороне параллелограмма, равна 180°⇒
угол ВАD=BCD=180°-120°=60°
Это синус 45°.
Угол ВАD=45°, угол АВD - прямой, следовательно, угол ВАD=45° и треугольник АВD равнобедренный.
Угол СВD=углу ВDА как накрестлежащий и равен 45°
( По т.Пифагора АВ также будет равна ВD)
СЕ - высота, СЕ⊥ ВD, след. угол ВСЕ=90°-45° =45°
и треугольник ВЕС равнобедренный, ВЕ=СЕ.
tg угла ECD= 3 ⇒
ЕD:ЕС=3
Но ЕС=ВЕ, следовательно,
ВD:ВЕ=3 ⇒
ВЕ -1 часть, ЕD-3 части.
ВЕ=ВD:4=(2√5):4=(√5):2